Если непрерывная кривая, имеющая в каждой точке касательную, пересекает ось Ox в точках  и
и 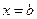 , то на этой кривой найдётся, по крайней мере, одна точка
, то на этой кривой найдётся, по крайней мере, одна точка 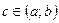 , в которой касательная параллельна оси Ox.
, в которой касательная параллельна оси Ox.
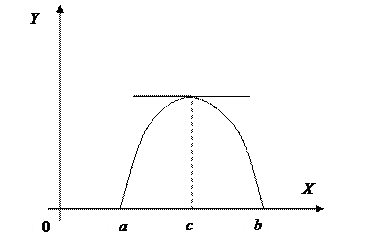
Замечание 1. Доказанная теорема остается справедливой и для такой дифференцируемой функции, которая на концах отрезка  не обращается в нуль, но принимает равные значения
не обращается в нуль, но принимает равные значения 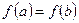 .
.
Замечание 2. Все три условия теоремы необходимы.
1) Нарушено первое условие, функция 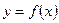 имеет разрыв в точке
имеет разрыв в точке 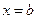 ,
, 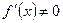 для всех
для всех  .
.
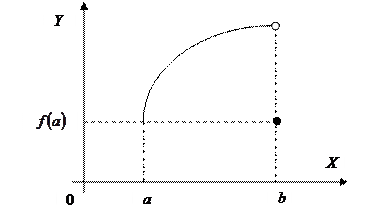
2) Нарушено второе условие теоремы, 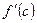 не существует,
не существует, 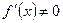 для всех
для всех 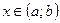 .
.

3) Нарушено третье условие теоремы, 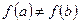 ,
, 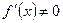 для всех
для всех 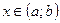 .
.
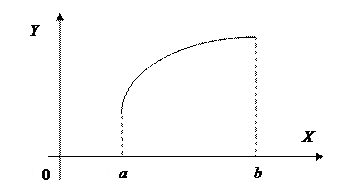
Пример: Проверим, применима ли теорема Ролля к функции  на отрезке
на отрезке 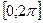 . Найдём точку c, в которой
. Найдём точку c, в которой 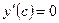 .
.
Функция 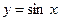 :
:
1) непрерывна на отрезке 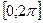 ;
;
2) дифференцируема на интервале  ,
, 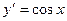 ;
;
3) 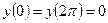 .
.
Тогда существует точка 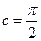 , такая, что
, такая, что  .
.
В качестве точки c можно выбрать также  .
.
Теорема о конечных приращениях (теорема Лагранжа)
Теорема Лагранжа. Если функция 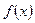 :
:
1) непрерывна на отрезке  ;
;
2) дифференцируема на интервале 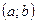 ;
;
то существует, по крайней мере, одна точка  , такая, что
, такая, что
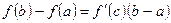 . (1)
. (1)
Геометрическая иллюстрация.
Из  :
:  . Таким образом, если во всех точках дуги AB существует касательная, то на этой дуге найдётся точка C между A и B, в которой касательная параллельна хорде, соединяющей точки A и B.
. Таким образом, если во всех точках дуги AB существует касательная, то на этой дуге найдётся точка C между A и B, в которой касательная параллельна хорде, соединяющей точки A и B.

Пример: Проверьте, применима ли теорема Лагранжа к функции 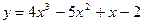 на отрезке
на отрезке 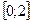 . Если окажется, что теорема применима, найдите точку c, в которой выполняется равенство (1).
. Если окажется, что теорема применима, найдите точку c, в которой выполняется равенство (1).
Решение. Функция 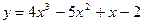 :
:
1) непрерывна на отрезке 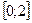 ;
;
2) дифференцируема на интервале 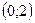 .
.
Тогда существует точка 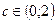 , такая, что выполняется равенство (1).
, такая, что выполняется равенство (1).
Находим значения 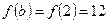 ,
, 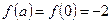 ,
, 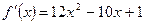 ,
, 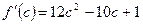 .
.
По формуле (1) получаем:

Находим корни квадратного уравнения  , т.е.
, т.е. 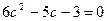 . Получаем
. Получаем  ,
,  , где
, где 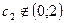 . Таким образом,
. Таким образом, 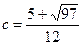 .
.
 2020-09-24
2020-09-24 300
300








