Теорема Коши. Если функция 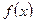 и
и 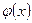 :
:
1) непрерывны на отрезке 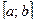 ;
;
2) дифференцируемы на интервале 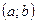 ;
;
3) 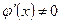 для всех
для всех 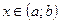 ;
;
то существует, по крайней мере, одна точка 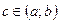 , такая, что
, такая, что
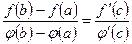 .
.
Пример: Пусть 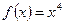 ,
, 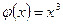 ,
, 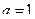 ,
, 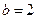 . Составьте формулу Коши и найдите значение c.
. Составьте формулу Коши и найдите значение c.
Решение. Проверим условия теоремы Коши:
1) 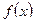 и
и 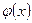 непрерывны на отрезке
непрерывны на отрезке 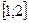 ;
;
2) 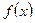 и
и 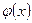 дифференцируемы на интервале
дифференцируемы на интервале 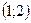 ;
;
3) 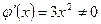 для всех
для всех 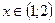 .
.
Тогда существует точка 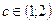 , такая, что
, такая, что 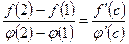 .
.
Находим значения 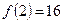 ,
, 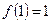 ,
, 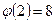 ,
, 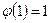 ,
, 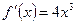 ,
, 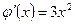 ,
, 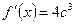 ,
, 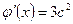 .
.
Получаем:
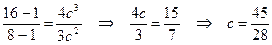 .
.
Правило Лопиталя
Теорема 1 (правило Лопиталя). Пусть функции 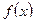 и
и 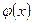 на некотором отрезке
на некотором отрезке 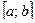 удовлетворяют условиям теоремы Коши и обращаются в нуль в точке
удовлетворяют условиям теоремы Коши и обращаются в нуль в точке 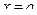 , то есть
, то есть 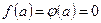 . Тогда, если существует предел отношения
. Тогда, если существует предел отношения 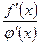 при
при 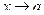 , то существует и
, то существует и 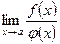 , причём
, причём
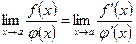 .
.
Теорема 1 применяется для раскрытия неопределённости вида 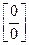 .
.
Примеры:
1) 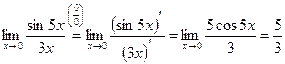
2) 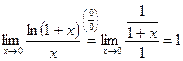
Замечание 1. Если 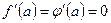 и производные и удовлетворяют тем условиям теоремы 1, которые были наложены на функции
и производные и удовлетворяют тем условиям теоремы 1, которые были наложены на функции 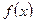 и
и 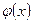 , то приходим к формуле
, то приходим к формуле
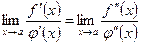 и т.д.
и т.д.
Замечание 2. Правило Лопиталя применимо и в том случае, если 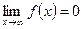 ,
, 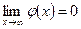 .
.
Теорема 2. Пусть функции 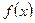 и
и 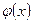 непрерывны и дифференцируемы при всех
непрерывны и дифференцируемы при всех 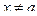 в окрестности точки
в окрестности точки 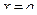 , причём производная
, причём производная 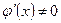 для точек данной окрестности,
для точек данной окрестности, 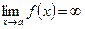 ,
, 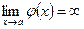 и существует
и существует 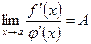 . Тогда существует
. Тогда существует 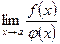 и
и
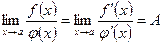 .
.
Теорема 2 применяется для раскрытия неопределённости вида 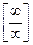 .
.
Замечание 3. Теорема 2 распространяется на случай, когда 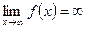 ,
, 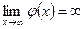 .
.
Пример:
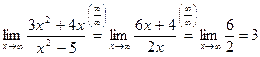
Замечание 4. Теоремы 1 и 2 справедливы, если предел отношения производных существует. Например,
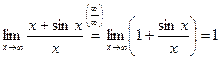
Найдём предел отношения производных:
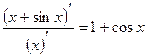 ,
, 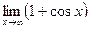 не существует.
не существует.
Теорема 2 не применима.
К неопределённостям вида 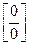 ,
, 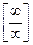 сводятся также другие неопределённости, такие, как
сводятся также другие неопределённости, такие, как 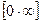 ,
, 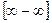 ,
, 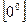 ,
, 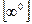 ,
, 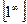 .
.
Пример:
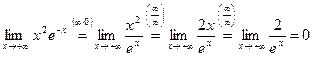
Тема 9. ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНОЙ
Условие постоянства функции.
Теорема 1. Если функция 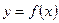 непрерывна на отрезке
непрерывна на отрезке 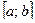 и во всех внутренних точках отрезка её производная равна нулю, то функция
и во всех внутренних точках отрезка её производная равна нулю, то функция 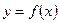 постоянна на этом отрезке.
постоянна на этом отрезке.
Теорема 2. Если функции 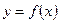 и
и 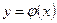 непрерывны на отрезке
непрерывны на отрезке 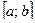 и имеют равные производные во всех внутренних точках отрезка, то разность этих функций постоянна:
и имеют равные производные во всех внутренних точках отрезка, то разность этих функций постоянна:
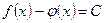
 2020-09-24
2020-09-24 147
147








