Возьмём на кривой  точку
точку 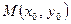 и напишем уравнение касательной к графику функции
и напишем уравнение касательной к графику функции 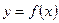 в точке
в точке 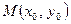 . Используем формулу:
. Используем формулу:
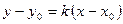 . (1)
. (1)
Для касательной угловой коэффициент  ,
, 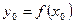 . Отсюда уравнение касательной к графику функции
. Отсюда уравнение касательной к графику функции 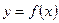 в точке
в точке 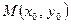 имеет вид:
имеет вид:
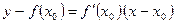
или
 . (2)
. (2)
Определение. Нормалью к кривой в данной точке называется прямая, проходящая через данную точку перпендикулярно к касательной в этой точке.
Согласно определению, угловой коэффициент нормали 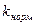 равен:
равен:
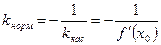 .
.
Подставив 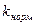 в уравнение (1), получим:
в уравнение (1), получим:
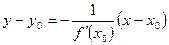
или
 . (3)
. (3)
Уравнение (3) есть уравнение нормали к графику функции  в точке
в точке  .
.
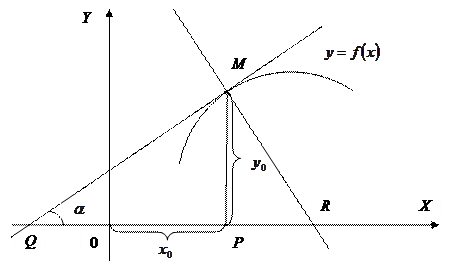
Длина отрезка QM, заключённого между точкой касания и осью Ox, называется длиной касательной, а проекция этого отрезка на ось Ox (отрезок QP) называется подкасательной. Длина отрезка MR называется длиной нормали, а проекция PR этого отрезка на ось Ox называется поднормалью.
Пример: Напишите уравнение касательной и нормали к кривой 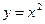 в точке
в точке 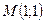 . Найдите длину подкасательной и поднормали.
. Найдите длину подкасательной и поднормали.
Решение.
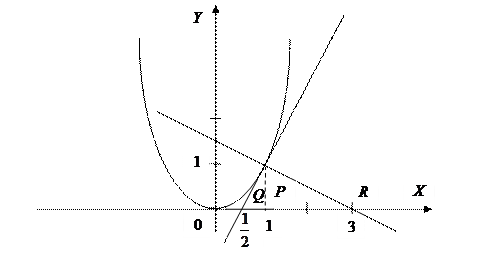
 ,
, 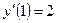 ,
, 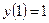 .
.
Получаем уравнение касательной 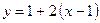 или
или 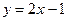 . Уравнение нормали имеет вид
. Уравнение нормали имеет вид 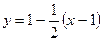 или
или 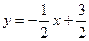 .
.
Находим координаты точек 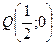 ,
, 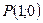 и
и 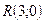 . Тогда длина подкасательной равна
. Тогда длина подкасательной равна 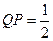 , а длина поднормали
, а длина поднормали 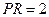 .
.
Дифференциал функции
Пусть функция 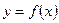 дифференцируема на отрезке
дифференцируема на отрезке 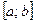 . Тогда для всех
. Тогда для всех 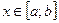 определена производная:
определена производная:
 .
.
Отсюда 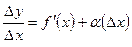 , где
, где 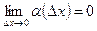 .
.
Тогда
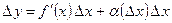 . (1)
. (1)
Так как в общем случае 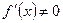 , то
, то
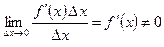 ,
, 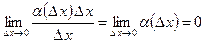 .
.
Таким образом,  есть бесконечно малая величина одного порядка малости относительно
есть бесконечно малая величина одного порядка малости относительно 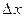 , а
, а 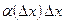 есть бесконечно малая величина высшего порядка относительно
есть бесконечно малая величина высшего порядка относительно  . Поэтому первое слагаемое приращения функции
. Поэтому первое слагаемое приращения функции  (по формуле (1)) есть главная часть приращения функции
(по формуле (1)) есть главная часть приращения функции 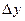 , линейная относительно
, линейная относительно 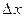 . Это выражение
. Это выражение  называют также дифференциалом функции
называют также дифференциалом функции 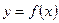 и обозначают через
и обозначают через 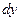 или
или 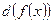 .
.
Таким образом,
 . (2)
. (2)
Если 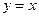 , то
, то 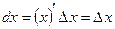 , отсюда
, отсюда 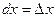 . Следовательно, дифференциал независимой переменной
. Следовательно, дифференциал независимой переменной 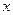 совпадает с её приращением. Формулу (2) можно записать в виде
совпадает с её приращением. Формулу (2) можно записать в виде
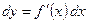 . (3)
. (3)
Отсюда
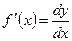 . (4)
. (4)
Формула (4) показывает, что производную 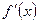 можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.
 2020-09-24
2020-09-24 190
190








