Возрастание и убывание функции

Теорема 1. Если функция 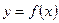 непрерывна на отрезке  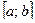и её производная положительна всюду на интервале , то 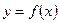 строго возрастает на .

Теорема 2. Если функция 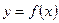 непрерывна на отрезке  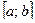и её производная отрицательна всюду на интервале , то 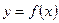 строго убывает на .

Пример: Найдите интервалы возрастания и убывания функции .

Решение. Найдём производную . Производная положительна в промежутке . Таким образом, функция возрастает во всей области определения.