Исследование функции на максимум и минимум с помощью второй производной

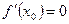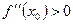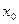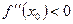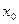Теорема. Пусть  и в точке существует вторая производная. Тогда, если , то  – точка минимума функции, а если , то  – точка максимума функции.

Пример: Исследуйте на экстремум функцию .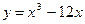

Решение.

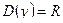
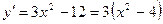
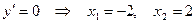 - критические точки.

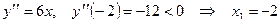 - точка максимума;

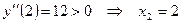           - точка минимума.

.

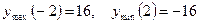Нахождение наибольшего и наименьшего значений функции на данном отрезке.

Если функция 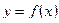 непрерывна на отрезке 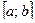, то на этом отрезке данная функция принимает и своё наибольшее, и своё наименьшее значения.

Для того чтобы найти наибольшее (наименьшее) значение функции 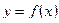 на отрезке 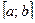, нужно:

1) найти производную данной функции;

2) найти критические точки;

3) вычислить значения функции в найденных точках и на концах отрезка;

4) из всех найденных значений выбрать наибольшее (наименьшее).

Пример: Найдите наибольшее и наименьшее значения функции 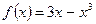 на отрезке .

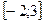Решение. Находим производную 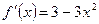 и критические точки 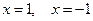. Определяем значения функции в критических точках и на концах отрезка:

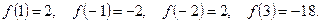
Из полученных значений выбираем наибольшее и наименьшее.

Итак, наибольшее значение функции на данном отрезке равно 2, а наименьшее -18.