Вычисление площадей плоских фигур
Площадь фигуры, заданной в декартовой системе координат.

| Площадь криволинейной трапеции, ограниченной непрерывной кривой 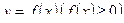 , двумя прямыми x = a, x = b и отрезком [ a; b ] оси OX вычисляется по формуле: , двумя прямыми x = a, x = b и отрезком [ a; b ] оси OX вычисляется по формуле:
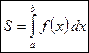 . .
|
Пример: Найдите площадь фигуры, ограниченной параболой 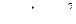 и осью OX.
и осью OX.

| Решение. Находим точки пересечения параболы с осью OX: 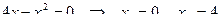 . Тогда искомая площадь равна: . Тогда искомая площадь равна:
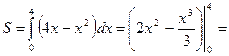 . .
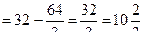
|

| Площадь фигуры, ограниченной двумя кривыми 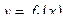 , , 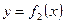 , , 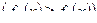 и двумя прямыми x = a, x = b, находится по формуле: и двумя прямыми x = a, x = b, находится по формуле:
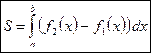 . .
|
Пример: Вычислите площадь фигуры, ограниченной линиями 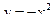 ,
, 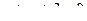 .
.
Решение. Находим точки пересечения линий: 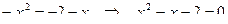 . Получаем
. Получаем  .
.
Вычисляем площадь:
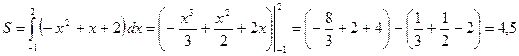 .
.

Пусть функция 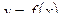 - непрерывна на [ a; b ] и
- непрерывна на [ a; b ] и 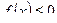 для всех
для всех 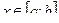 . Рассмотрим фигуру Ф, симметричную фигуре F относительно оси OX.
. Рассмотрим фигуру Ф, симметричную фигуре F относительно оси OX.
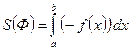 ,
, 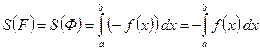 .
.
Таким образом, 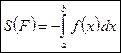 .
.

| 
|
Если 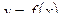 конечное число раз меняет знак на отрезке [ a; b ], то интеграл по отрезку [ a; b ] разбиваем на сумму интегралов по частичным отрезкам. Интеграл будет положителен на тех отрезках, где
конечное число раз меняет знак на отрезке [ a; b ], то интеграл по отрезку [ a; b ] разбиваем на сумму интегралов по частичным отрезкам. Интеграл будет положителен на тех отрезках, где 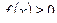 , и отрицателен там, где
, и отрицателен там, где 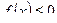 . Тогда сумма площадей вычисляется по формуле:
. Тогда сумма площадей вычисляется по формуле:
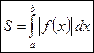 .
.
2. Площадь фигуры, ограниченной кривой, заданной параметрическими уравнениями.
Пусть криволинейная трапеция ограничена кривой, заданной в параметрической форме 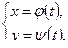 где
где 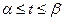 ,
, 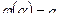 ,
, 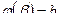 .
.

| Данные уравнения определяют некоторую функцию 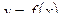 на отрезке [ a; b ]. Так как на отрезке [ a; b ]. Так как 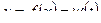 , а , а 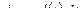 , получаем: , получаем: 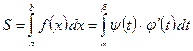 . Таким образом, . Таким образом,
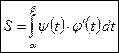 . .
|
Пример: Вычислите площадь области, ограниченной эллипсом  .
.
Решение.
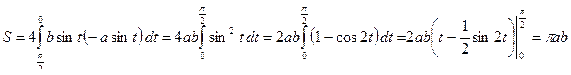 .
.

Площадь криволинейного сектора в полярных координатах.

| Пусть в полярной системе координат задана кривая 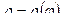 , где , где  – непрерывная функция при – непрерывная функция при 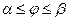 . Площадь сектора OAB, ограниченного кривой . Площадь сектора OAB, ограниченного кривой 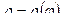 и радиусами-векторами и радиусами-векторами 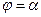 и и  , вычисляется по формуле: , вычисляется по формуле:
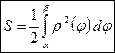 . .
|
Пример: Найдите площадь фигуры, ограниченной улиткой Паскаля 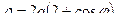 .
.

| 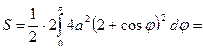
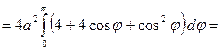
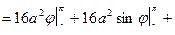
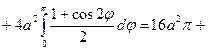
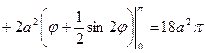
|
 2020-09-24
2020-09-24 85
85








