Вычисление длины дуги плоской кривой

 

Если кривая 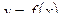 на отрезке [ a; b ] – гладкая (т.е. производная  непрерывна), то длина соответствующей дуги этой кривой находится по формуле

.

Пример: Вычислите длину дуги цепной линии  от  до .

Решение. ,     ,

Тогда

.

При параметрическом задании кривой , , где  и  – непрерывно дифференцируемые функции, длина дуги кривой, соответствующая изменению параметра t от  до  выражается интегралом

.

Если гладкая кривая задана в полярных координатах уравнением 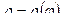, где 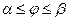, то длина дуги равна

.

 

Вычисление объёма тела вращения

 

Если криволинейная трапеция, ограниченная кривой 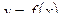 и прямыми x = a, x = b, вращается вокруг оси OX, то объем тела вращения вычисляется по формуле

.

Если криволинейная трапеция, ограниченная кривой  и прямыми y = c, y = d, вращается вокруг оси OY, объем тела вращения равен

.

Пример: Вычислите объём тела, полученного от вращения фигуры, ограниченной параболой , вокруг оси OX.

Решение.

.

 

Вычисление площади поверхности вращения

 

Если дуга гладкой кривой 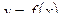 вращается вокруг оси OX, то площадь поверхности вращения вычисляется по формуле

.

Если кривая задана параметрическими уравнениями , , где , то площадь поверхности вращения равна

.

Если кривая задана в полярных координатах уравнением 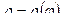, где 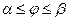, то площадь поверхности вращения равна

.

Пример: Найти площадь поверхности, образованной вращением параболы  вокруг оси абсцисс от вершины до точки с абсциссой x =3 a.

Решение. , , .

РАЗДЕЛ 5. варианты контрольных работ

Самостоятельная работа №1 по теме «Непосредственное интегрирование»

Вариант №1

1)              2)

Вариант №2

1)         2)

Вариант №3

1)                    2)

Вариант №4

1)             2)

Вариант №5

1)              2)

Вариант №6

1) 2)

Вариант №7

1)   2)

Вариант №8

1) 2)

Вариант №9

1)      2)

Вариант №10

1) 2)

Вариант №11

1) 2)

Вариант №12

1)                   2)

Вариант №13

1)               2)

Вариант №14

1)           2)

Вариант №15

1)                2)

Вариант №16

1)         2)

Вариант №17

1)                2)

Вариант №18

1)                2)

Вариант №19

1)                   2)

Вариант №20

1)             2)

Вариант №21

1)              2)

Вариант №22

1)           2)

Самостоятельная работа №2 по теме «Замена переменной под знаком неопределённого интеграла»

Вариант №1

1) 2)

Вариант №2

1) 2)

Вариант №3

1) 2)

Вариант №4

1)                 2)

Вариант №5

1) 2)

Вариант №6

1)      2)

Вариант №7

1) 2)

Вариант №8

1)              2)

Вариант №9

1)          2)

Вариант №10

1)              2)

Вариант №11

1)                   2)

Вариант №12

1)                   2)

Вариант №13

1)   2)

Вариант №14

1) 2)

Вариант №15

1)   2)

Вариант №16

1)   2)

Вариант №17

1) 2)

Вариант №18

1) 2)

Вариант №19

1)   2)

Вариант №20

1)   2)

Вариант №21

1) 2)

Вариант №22

1) 2)

Вариант №23

1)      2)

Вариант №24

1) 2)