Пусть некоторый опыт может приводить лишь к одному из конечного множества результатов. Эти результаты будем называть элементарными исходами. Предположим, что элементарные исходы удовлетворяют следующим условиям:
1) образуют полную группу, т.е. в каждом испытании обязан появиться какой-нибудь из этих исходов;
2) попарно несовместны, т.е. два различных элементарных исхода не могут появиться в одном испытании;
3) равновозможны, т.е. шансы появления у всех элементарных исходов одинаковы.
В этих условиях может быть использовано классическое определение вероятности.
Вероятностью события А называется число Р(А), равное отношению числа исходов испытания, благоприятствующих событию А к общему числу исходов:
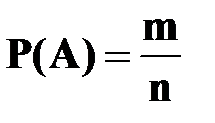 ,
,
где n - общее число исходов испытания; m – число исходов, благоприятствующих событию А, т. е. число элементарных исходов, в которых появляется событие А.
Из классического определения вероятности следует, что вероятность любого события заключена между нулем и единицей, т. е.
0 ≤ Р(А) ≤ 1.
Пример 2.1 В урне находится 12 белых и 8 черных шаров. Какова вероятность того, что наудачу вынутый шар будет белым?
Решение. Опыт состоит в выборе наудачу одного шара из урны. Число всех равновозможных исходов опыта равно: n = 12+8= 20.
Рассмотрим событие А – вынут белый шар.
Число исходов, благоприятствующих событию А, равно: m=12. Следовательно, по формуле классического определения вероятности имеем:
P(A)= 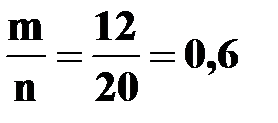 .
.
3. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ
Событие, которое в результате опыта должно произойти непременно, называется достоверным событием.
Событие, которое в данном опыте не может произойти, называется невозможным.
Вероятность достоверного события равна единице, вероятность невозможного события равна нулю.
Два события называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.
Противоположным событию А называется событие 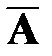 состоящее в том, что в результате опыта событие А не наступит.
состоящее в том, что в результате опыта событие А не наступит.
Суммой событий А и В называется событие С=А+В, состоящее в наступлении хотя бы одного из них, т.е. или события А, или события В, или А и В вместе.
Если события А и В несовместны, то С=А+В – это событие А, или В.
Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Произведением событий А и В называется событие С=А 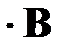 , состоящее в совместном появлении и события А, и события В.
, состоящее в совместном появлении и события А, и события В.
Два события называются независимыми, если вероятность одного из них не зависит от появления или непоявления другого события.
Два события называются зависимыми, если вероятность одного из них зависит от появления или непоявления другого события.
Если А и В – зависимые события, то вероятность события В, вычисленную в предположении, что событие А уже наступило, называют условной вероятностью и обозначают PA(B).
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любой совокупности остальных.
Теорема сложения вероятностей несовместных событий. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Р(А+В) = Р(А)+Р(В).
Следствие 1. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A1+A2+…+An)=P(A1) + P(A2)+…+P(An).
Следствие 2. Если события А1, А2, А3,…, Аn попарно несовместны и образуют полную группу событий, то сумма их вероятностей равна единице:
P(A1)+P(A2)+P(A3)+…+P(An) =1.
Следствие 3. Сумма вероятностей противоположных событий равна единице:
P(A) + P(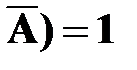 .
.
Теорема сложения вероятностей совместных событий. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
Р(А+В) = Р(А)+Р(В) – Р(А 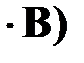 .
.
Теорема может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий:
P(A+B+C)=P(A)+P(B)+P(C) – P(A∙B) – P(A∙C) – P(B∙C)+ P(A∙B∙C).
Проще, однако, найти вероятность суммы нескольких совместных событий P(S)=P(A1+A2+A3+…+An), используя равенство P(S)+P(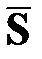 )=1, где
)=1, где 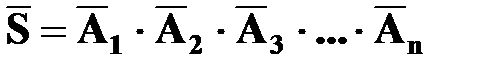 - противоположно событию S. Тогда P(S)= 1-P(
- противоположно событию S. Тогда P(S)= 1-P(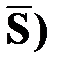 .
.
Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
Р(А∙В)=Р(А)∙Р(В).
Следствие 1. Вероятность появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
P(A1∙A2∙A3∙…∙An) =P(A1)∙P(A2)∙P(A3)∙…∙P(An).
Следствие 2. Вероятность появления хотя бы одного из событий А1, А2, А3, …, Аn, независимых в совокупности, равна разности единицы и произведения вероятностей противоположных событий 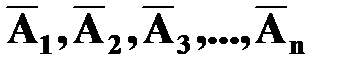 :
:
Р(А1+ А2+ А3…+Аn)= 1 – Р(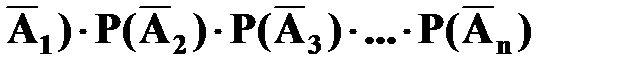 .
.
Теорема умножения вероятностей зависимых событий. Вероятность совместного появления двух зависимых событий равна произведению вероятности появления одного из них на условную вероятность другого, вычисленную в предложении, что первое событие уже наступило:
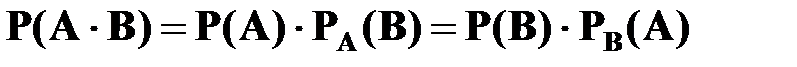 .
.
Следствие. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности появления одного из них на условные вероятности всех остальных, причем вероятности каждого последующего события вычисляются в предположении, что все предыдущие события уже наступили:
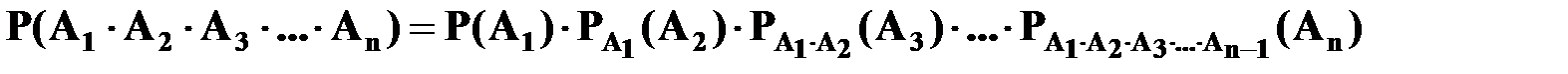 ,
,
где 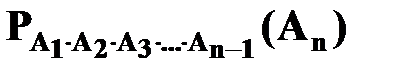 - вероятность появления события Аn, вычисленная в предположении, что события А1, А2, А3, …, Аn-1 наступили.
- вероятность появления события Аn, вычисленная в предположении, что события А1, А2, А3, …, Аn-1 наступили.
Например, для трех зависимых событий
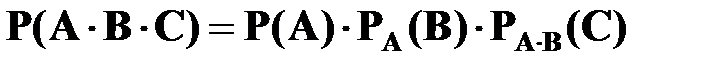 .
.
Пример 3.1 Произведен залп из двух орудий по мишени. Вероятность попадания из первого орудия равна 0,85, а из второго – 0,91. Найти вероятность поражения мишени.
Решение.
Пусть событие А – поражение мишени, событие А1 - поражение мишени из первого орудия, событие А2 – поражение мишени из второго орудия. Тогда А=А1+А2. Поскольку события А1 и А2 совместны, то
P (A) =Р (А1+ А2) = Р (A1) + P (A2) – P (A1∙A2).
Так как события А1 и А2 независимы,
то 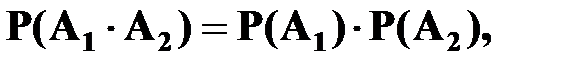 где P(A1)=0,85,
где P(A1)=0,85,
а P(A2)=0,91 по условию задачи.
Следовательно,
P (A) =0,85+0,91 – 0,85∙0,91=0,9865.
 2020-09-24
2020-09-24 103
103








