Определение предела числовой последовательности

Определение. Число а называется пределом последовательности {х_п}, если для .

Если последовательность имеет своим пределом число а, то пишут , или  при .

В этом случае говорят, что последовательность {х_п}, сходится к числу а.

Символическая запись определения:

:  [28].

Геометрическая интерпретация предела последовательности

Интерпретация – латинское слово: в переводе означает «истолкование, разъяснение смысла, значения чего-то».

Так как числовую последовательность можно рассматривать как после-довательность точек на прямой, то о пределе последовательности можно го-ворить как о точке на прямой.

Неравенство 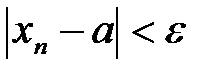 равносильно неравенству , которое в свою очередь равносильно такому , х_п [28].

А интервал   называют ε-окрестностью точки а и обознача-етсяU(а, ε).

Тот факт, что число а есть предел последовательности {х_п} геометрии-чески означает, что в любой ε- окрестности точки а находятся все члены пос-ледовательности {х_п}, начиная с некоторого элемента под номером n>N.

А вне ε- окрестности точки а может находиться лишь конечное число членов последовательности

 

Рис.2.

Если взять , то - окрестность  будет также меньше окрестности . Следовательно, в - окрестность или интервал  попадут элементы последовательности, начиная с более высо-кого номера.

Рис.3.

Точка, изображающая предел а, является как бы сосредоточением сгуст-ка точек, изображающих значения последовательности [28].

Неравенство Бернулли

Якоб Бернулли - швейцарский математик (1654-1705).

Лемма (неравенство). Для любого натурального числа   справед-ливо неравенство при :                                    (2)

Доказательство.

1. Доказательство проведем методом математической индукции.

2. При  соотношение (2) очевидно: .

3. Предположим, что соотношение (2) справедливо при :

.

4. Докажем это неравенство при .

5. Для этого умножим обе части неравенства  на поло-жительное число , так как  по условию леммы.

6. Получим .

7. Выполним элементарные преобразования .

8. Сгруппируем 2 и 3 слагаемые правой части неравенства:

9. Сравним два выражения .

10. При  и , очевидно, что >  на .

11.  тем более.

Таким образом, неравенство доказано при .  Лемма доказана.

Замечание. Если в неравенстве  принять , то при  неравенство примет вид: ,  [27].