Определение. Последовательность {xn} называется бесконечно боль-шой, если для любого положительного числа М существует номер N такой, что при  п>N выполняется неравенство
п>N выполняется неравенство 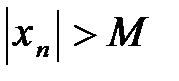 .
.
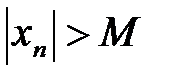

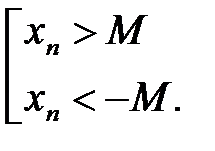
{xn} – бесконечно большая 
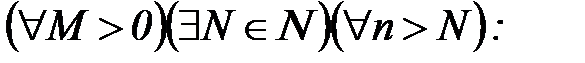
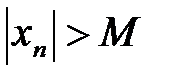 .
.
В этом случае пишут 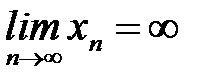 .
.
Причем:
а) Если последовательность {xn} такова, что для любого числа 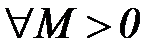 существует такой номер элемента N, что при всех
существует такой номер элемента N, что при всех  п>N выполняется неравенство
п>N выполняется неравенство 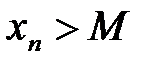 , то пишут
, то пишут  .
.
б) Если последовательность {xn} такова, что для любого числа 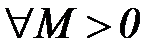 существует такой номер элемента N, что при всех
существует такой номер элемента N, что при всех  п>N выполняется неравенство
п>N выполняется неравенство 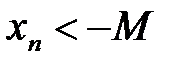 , то пишут
, то пишут 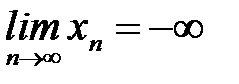 .
.
Но во всех указанных случаях говорят, что последовательность {xn} имеет бесконечный предел, равный соответственно: 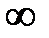 ;
; 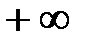 ;
; 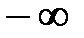 . Если
. Если 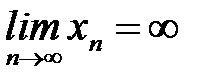 или
или  , или
, или 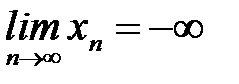 , то последовательность является бесконечно большой [28].
, то последовательность является бесконечно большой [28].
Замечание.
1. Очевидно, что бесконечно большая последовательность не имеет пре-дела в том смысле, как мы его определяли и обозначали числом а. Использование слова «предел» и обозначение «lim» является лишь тради-ционным.
2. В дальнейшем всегда под словом «предел» последовательности будем понимать конечный предел, т.е. определенное число а.
3. Термин «сходящаяся последовательность» употребляется для после-
довательности, имеющей конечный предел.
Окрестность беззначной бесконечности
Придадим определениям конечного и бесконечных пределов последова-тельности единообразную форму с помощью понятия «окрестность».
Определение. Для 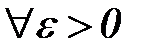
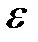 - окрестностью бесконечности без знака
- окрестностью бесконечности без знака 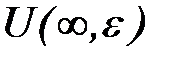 равна:
равна: 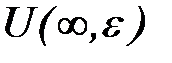
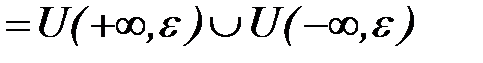 . Иногда
. Иногда 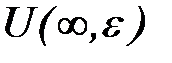 обозначают просто
обозначают просто  , а говорят окрестность бесконечности [29].
, а говорят окрестность бесконечности [29].
На координатной прямой:

Рис.4.
 2020-10-10
2020-10-10 293
293








