Определение. Последовательность, у которой существует предел назы-вается сходящейся.
Иными словами: последовательность {хп} является сходящейся, если  такое число а, что для
такое число а, что для  найдется такой номер
найдется такой номер 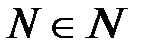 , что для всех
, что для всех  выполняется неравенство:
выполняется неравенство: 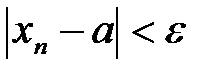 .
.
{хп} – сходится 


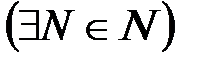
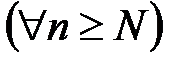 :
: 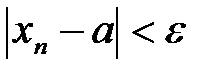 .
.
Замечание.
1. Величина п зависит от того, каково  , которое выбирается произ-вольно.
, которое выбирается произ-вольно.
2. Чем меньше 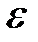 , тем п будет больше. Исключением является слу-чай, когда последовательность состоит из одинаковых элементов.
, тем п будет больше. Исключением является слу-чай, когда последовательность состоит из одинаковых элементов.
3. Если N1>N и неравенство 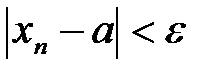 выполняется при
выполняется при 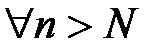 , то неравенство подавно будет выполняться и при
, то неравенство подавно будет выполняться и при  [28].
[28].
Определение. Последовательность, которая не является сходящей-ся, называется расходящейся.
Замечание.
1. Если  и
и 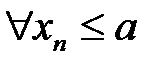 при
при  , то говорят, что последова-тельность {хп} сходится к числу а слева. И пишут вместо
, то говорят, что последова-тельность {хп} сходится к числу а слева. И пишут вместо 
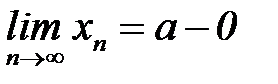 .
.
2. Если  и
и 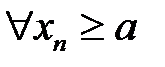 при
при  , то говорят, что последова-тельность {хп} сходится к числу а справа. И пишут вместо
, то говорят, что последова-тельность {хп} сходится к числу а справа. И пишут вместо 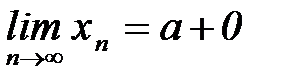 .
.
Примеры, иллюстрирующие различные стремления последователь-ности к своему пределу.
Пример №1. Доказать, что последовательность  при
при 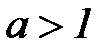 стремится к 1.
стремится к 1.
Пример №2. Доказать, что последовательность 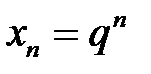 при
при  стремится к 0.
стремится к 0.
Пример №3. Доказать, что последовательность  не имеет предела.
не имеет предела.
Доказательство провести самостоятельно.
 2020-10-10
2020-10-10 238
238








