2020-10-10
151
Определение. Элемент а, являющийся действительным числом или од-ной из бесконечностей (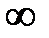 
; 
; 
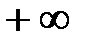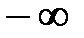) называется пределом последовате-льности {хп}, если какова бы ни была 
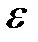- окрестность элемента а 
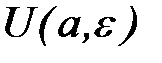, для нее существует номер N такой, что при п > N справедливо утвержде-ние: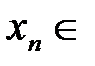 
.
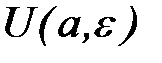Определение. Если последовательность {xn} такова, что все ее эле-менты равны между собо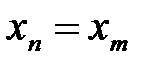й: 
при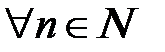 
, 
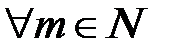, то она называ-ется стационарной или постоянной [29].
Единственность предела сходящейся последовательности
Теорема. Последовательность точек расширенной числовой прямой может иметь на этой прямой только один предел.
Доказательство.
1. Используем для доказательства метод от противного.
2. Пусть существует последовательность {xn}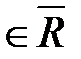 
, у которой имеются, по крайней мере, два различных предела: а 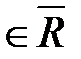, b .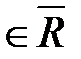
3. Выберем произвольные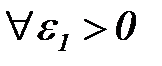 
и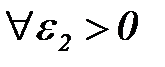 
так, чтобы 
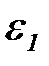- окрестно-сть точки а не пересекалась с 
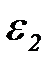- окрестностью точки b. Это всегда мож-но сделать согласно лемме о непересекающихся окрестностях.
4. В соответствии с определением предела:
а) если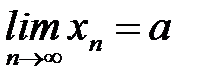 
, то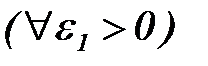 
: 
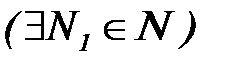
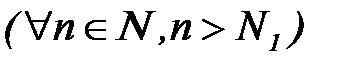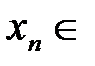
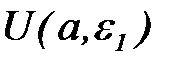
б) если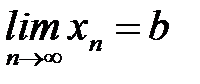 
, то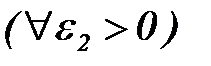 
: 
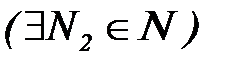
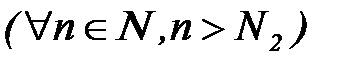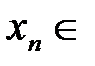
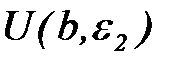
5. Обозначим через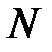 
наибольший из номеров элементов последователь-ност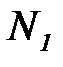и 
и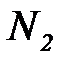 
: 
.
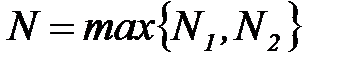6. Тогда для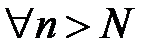 
будет одновременно выполняться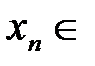 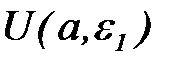и
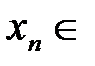
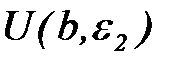, следовательно, окрестности должны пересекаться:
.
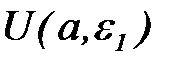
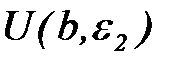7. Но это противоречит лемме. Ведь 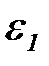- окрестность точки а при пере-сечении с 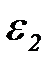- окрестностью точки b дает пустое множество.
8. Полученное противоречие показывает, что принятое утверждение неверно и что теорема доказана [28].
Следствие. Числовая последовательность может иметь только один предел, конечный или бесконечный определенного знака.
Следствие является частным случаем теоремы [28].
Модуль
Тема №2
Предел последовательности
Лекция №5
1. Ограниченность сходящейся последовательности.
2. Переход к пределу в неравенствах.
3. Теорема о пределе сжатой переменной.
4. Теорема о необходимом и достаточном условии сходимости последовательности к числу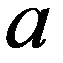 
.
5. Бесконечно малые последовательности.
6. Свойства бесконечно малых последовательностей.
7. Связь между бесконечно малыми и бесконечно большими последовательностями.
