Ограниченность сходящейся последовательности

Определение. Последовательность {x_n} называется ограниченной свер-ху, если существует число М такое, что для всех элементов последователь-ности выполняется неравенство: .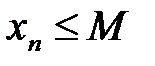

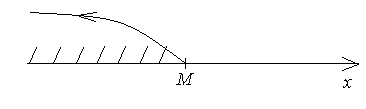
Рис.5.

Все элементы последовательности 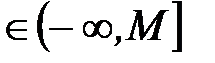 (лежат левее точки М).

Пример. 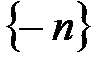 ограничена сверху , .

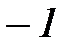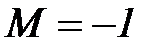Определение. Последовательность {x_n} называется ограниченной сни-зу, если существует число т такое, что для всех элементов последователь-ности выполняется неравенство: .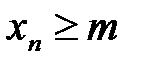

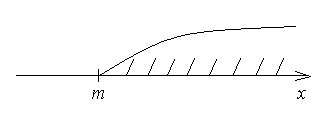
Рис.6.

Все элементы последовательности 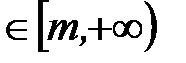 (лежат правее точки т) [28].

Пример. 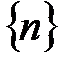 ограничена снизу , .

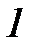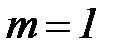Определение. Последовательность 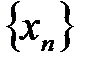 называется ограниченной, если она ограничена и сверху, и снизу, т.е. существуют числа т и М такие, что любой элемент x_n этой последовательности удовлетворяет неравенствам .

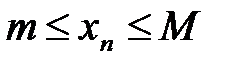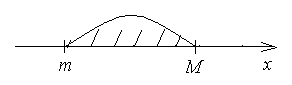
Рис.7.

Все элементы последовательности .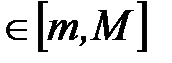

Пример. 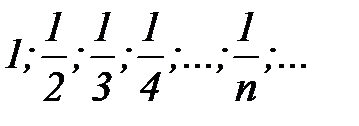  ограничена, так как для любого элемента последовательности выполняется неравенство , , .

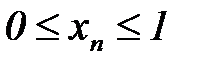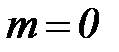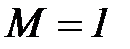Определение. Последовательность 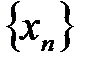 называется неограниченной св-ерху (снизу), если она не является ограниченной сверху (снизу). [30].

Неограниченная последовательность сверху (снизу) может быть ограни-чена снизу (сверху).

Теорема. Если последовательность имеет предел, то она ограниче-на.

Доказательство.

1. Пусть 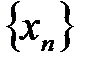 – сходящаяся последовательность, а число а – ее пре-дел.

2. Выберем .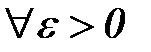

3. Тогда существует такое натуральное число N, что 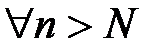 будет выполняться неравенство .

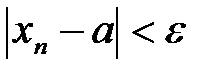4. Прибавим к левой и правой частям неравенства по положительному числу : .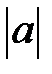

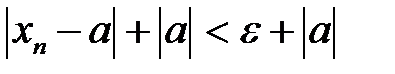5. Воспользуемся свойством модуля суммы двух действительных чи-сел .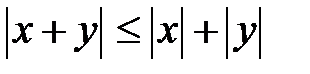

6. Тогда левая часть неравенства пункта 4 примет вид: .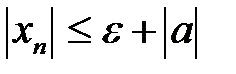

7. Примем за 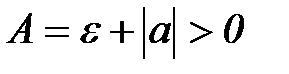, тогда 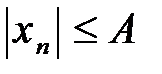,  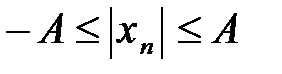- условие ограниченности последовательности. Значит последовательность  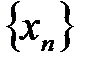– ограничена, если имеет предел [29].

Ч.т.д.