Связь между бесконечно большими и бесконечно

 малыми последовательностями

Теорема: Если 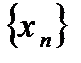  – бесконечно большая последовательность и все её элементы отличны от нуля, то последовательность   – бесконечно малая. И наоборот: если 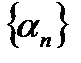  – бесконечно малая и все её элементы отличны от нуля, , то   – бесконечно большая последовательность.

Доказательство: 1.Пусть 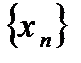 – бесконечно большая последовательность и , . Требуется доказать, что  – бесконечно малая последовательность.

2.Возьмем . И примем .

3.Согласно определению бесконечно большой последовательности

 или , или .

4.По свойству модуля частного двух действительных чисел можно записать  или , значит,  – бесконечно малая последовательность при .

Ч.т.д.

Замечание: Доказательство второй части теоремы проводится аналогично.