Переход к пределу в неравенствах

(Теорема о предельном переходе в неравенствах)

Теорема. Если элементы сходящейся последовательности 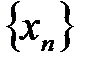, начиная с некоторого номера, удовлетворяют неравенству  (), то и пре-дел а этой последовательности удовлетворяет неравенству  ().

Доказательство.

1.Пусть все элементы сходящейся последовательности 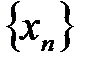, начиная с

 некоторого номера, удовлетворяют неравенству 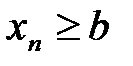. Требуется доказать, что 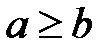, где а – предел последовательности.

2. Предположим обратное, то есть что а < b.

3.Так как а — предел последовательности 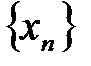, то для  ()

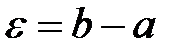 существует такой номер последовательности N, что при n>N выполняется неравенство  или .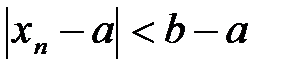

4. Последнее неравенство равносильно следующему двойному неравен-ству .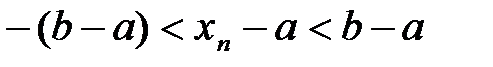

5.Рассмотрим правую часть неравенства 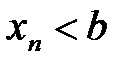. А по условию теоремы .

6. Полученное противоречие доказывает теорему [29].

Ч.т.д.

Замечание. Случай   доказывается аналогично.

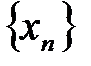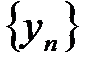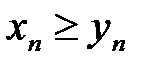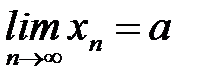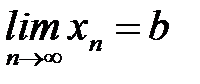Следствие. Если для двух последовательностей  и всегда вы-полняется неравенство , причем каждая из них имеет конечный пре-дел,  и , то .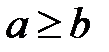

Доказательство.

1. Будем доказывать методом от противного, т.е. пусть 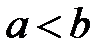 при .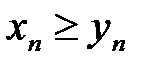

2. Возьмем число 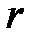 между а и b в силу непрерывности действительных чисел, т.е. .

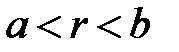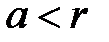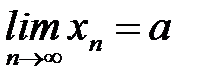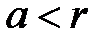3. Рассмотрим левую часть двойного неравенства: . Так как по усло-вию теоремы  и , то в силу теоремы о предельном переходе в неравенствах найдется такое , что 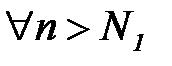 будет выполняться неравен-ство .

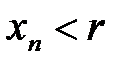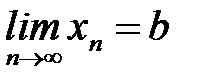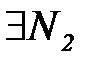4. Рассмотрим правую часть двойного неравенства: . Так как по ус-ловию теоремы  и , то в силу теоремы о предельном переходе в неравенствах найдется такое , что 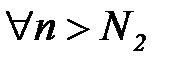 будет выполняться неравен-ство .

5. Если за N обозначить наибольший из номеров 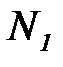 и 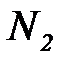, то есть

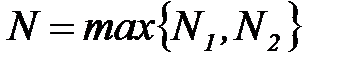, то для  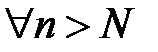будут одновременно выполняться оба нера-венства:  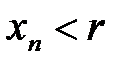и , .

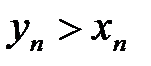6. А по условию теоремы 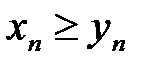. Полученное противоречие доказывает

 следствие к теореме [28].

Ч.т.д.

Теорема о пределе сжатой переменной

Теорема. Пусть даны три последовательност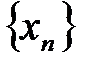и ,   и , при-чем 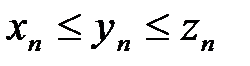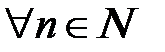. Пусть последовательност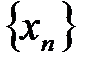и  и 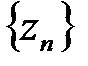 имеют один и тот же предел а: 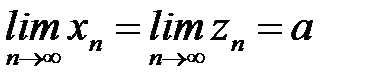. Тогда последовательность  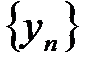так-же имеет предел а: .

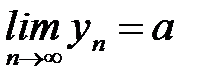Доказательство.

1. Возьмем любое .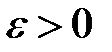

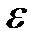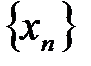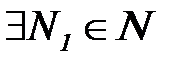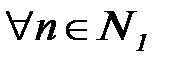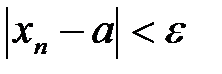
2. По этому числу  для последовательности  найдется такой номер , что : .                               (3)

3. По этому жечислу 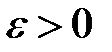 для последовательности  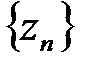найдется номер 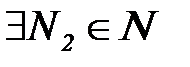, что n>N₂ будет выполняться неравенство:

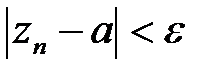
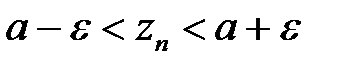 .                                                            (4)

4. Обозначим через N наибольший номер из N₁ и N₂: .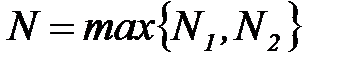

5. Тогда при n>N будут выполняться одновременно два неравенства

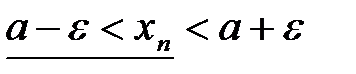 и  .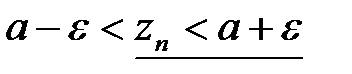

6. Подчеркнем левую часть первого неравенства и правую часть второго неравенства.

7. Используя подчеркнутые неравенства, а также неравенства, данные в условии теоремы, получаем 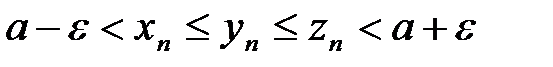 при n>N. Отсюда  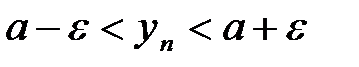или 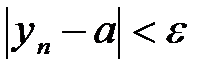 при n>N. Это означает, что  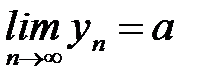[28].

Ч.т.д.

14.Теорема о необходимом и достаточном условии сходимости последовательности к числу а

Огюстен Луи Коши – французский математик (1798 - 17857).

До сих пор не было дано достаточно общего критерия, с помощью кото-рого можно было бы узнать, сходится или нет данная последовательность.

Само определение предела последовательности содержит значение пре-дела, которое может быть неизвестным.

Необходимо иметь такой критерий для определения сходимости и рас-ходимости последовательности, который базировался бы только на свойствах элементов данной последовательности.

Теорема о необходимом и достаточном условии сходимости последова-тельности дает как раз подобный критерий.

Определение. Последовательность 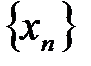 удовлетворяет условию Коши, если для любого  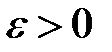существует такой номер 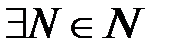, что для всех номеров  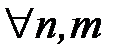удовлетворяющих неравенству  и 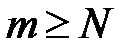, справедливо неравенство:

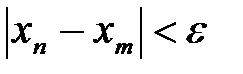                                   .                                                    (5)

Определение. Последовательность, удовлетворяющая условию Коши, называется фундаментальной последовательностью [29].

Теорема (Критерий Коши). Для того, чтобы последовательность схо-дилась необходимо и достаточно, чтобы она удовлетворяла условию Коши.

Доказательство необходимости.

1. Пусть последовательность 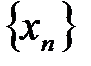 сходится, т.е. 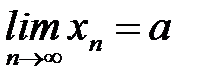. Требуется доказать, что эта последовательность удовлетворяет условию Коши.

2. Зададим произвольное  ().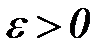

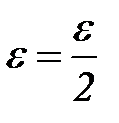3. Тогда согласно определению предела последовательности существует такой номер элемента , что 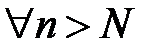 выполняется неравенство

.

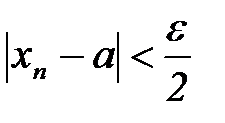4. Возьмем еще один номер элемента , тогда должно выполняться неравенство .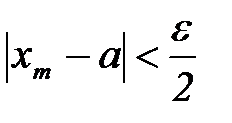

5. Сложим два неравенства п.3. и п.4.: .

6. Воспользуемся свойством модуля разности двух действительных чисел (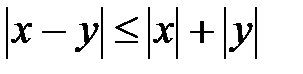):   или 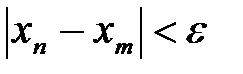 - это неравенство говорит о том, что последовательность удовлетворяет условию Коши [29].

Ч.т.д.