Свойства бесконечно малых последовательностей

Теорема №1. Алгебраическая сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Доказательство: 1.Пусть последовательности 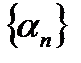 и  – бесконечно малые последовательности. Требуется доказать, что 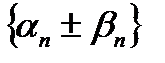 – бесконечно малая последовательность.

2.Выберем .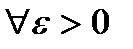

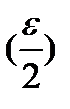3.Пусть  – номер, начиная с которого , а  – номер, начиная с которого  (в соответствии с определением бесконечно малой последовательности такие номера найдутся).

4.Возьмем  наибольшим из  и , т.е. .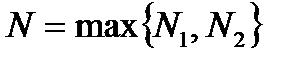

5.Тогда при  будут выполняться одновременно два неравенства:

 и .

6.Сложим эти два неравенства  или .

7.Воспользуемся свойством модуля суммы и разности двух действительных чисел:  и :  или  – а это условие того, что последовательность 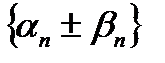 является бесконечно малой последовательностью при .

Ч.т.д.

Следствие к теореме №1. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Это утверждение следует из доказательства теоремы №1 на основе метода математической индукции.

Теорема №2. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Доказательство: 1.Пусть  и  – бесконечно малые последовательности. Требуется доказать, что  – бесконечно малая последовательность.

2.Так как последовательность 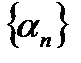 – бесконечно малая, то по определению бесконечно малой последовательности: : .

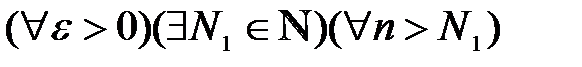3.Так как последовательность  – бесконечно малая, то по определению бесконечно малой последовательности: : .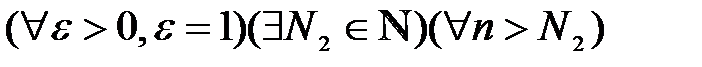

4.Выберем  наибольшим из  и , т.е. .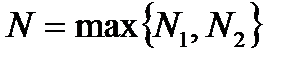

5.Тогда при всех  будут выполняться одновременно два неравенства:  и .

6.Перемножим эти два неравенства  или в соответствии со свойством модуля произведения двух действительных чисел  или, 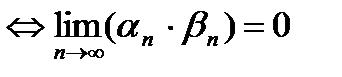, т.е. последовательность  – бесконечно малая последовательность при .

Ч.т.д.

Следствие к теореме №2. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Данное утверждение следует из доказательства теоремы на основе метода математической индукции.

Теорема №3. Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.

Доказательство: 1.Пусть 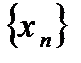 – ограниченная последовательность, а

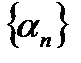 – бесконечно малая последовательность. Требуется доказать, что

 – бесконечно малая последовательность.

2.Так как последовательность 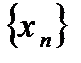 ограничена, то  такое число , что для любого элемента последовательности выполняется неравенство: .

3.Возьмем .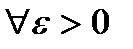

4.Так как последовательность  бесконечно малая, то по определению бесконечно малой последовательности , что 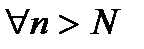 выполняется неравенство  или .

5.Перемножим неравенства п.2 и п.4:  или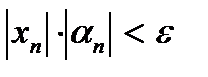

6.По свойству модуля произведения двух действительных чисел: 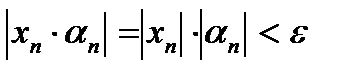 или 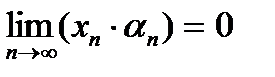, а это означает, что  – бесконечно малая последовательность при .

Ч.т.д.