1. Пусть последовательность 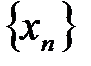 удовлетворяет условию Коши, т.е.
удовлетворяет условию Коши, т.е. 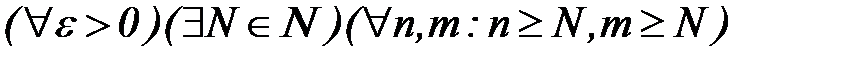 :
: 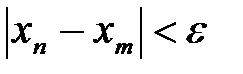 . Надо доказать, что последовательность
. Надо доказать, что последовательность 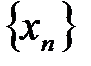 сходится к числу а.
сходится к числу а.
2. Возьмем 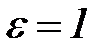 .
.
3. Тогда 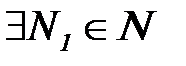 , что
, что 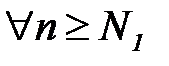 и
и 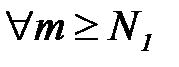 выполняется неравенство
выполняется неравенство
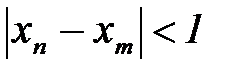 .
.
4. В частности, если 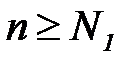 , а
, а 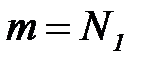 , то будет выполняться неравенство
, то будет выполняться неравенство 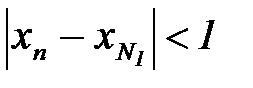 или
или 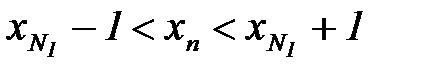 при
при 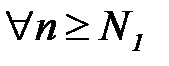 .
.
5. Это означает, что последовательность 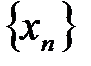 с номерами:
с номерами: 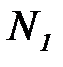 ,
, 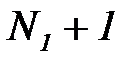 ,
, 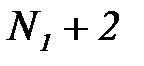 ,
, 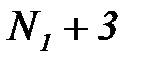 ,
, 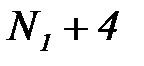 , … ограничена.
, … ограничена.
6. Согласно теореме, если последовательность ограничена, то она сходи-тся, т.е. имеет предел, например, а: 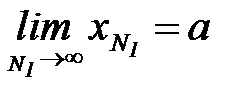 .
.
7. Тогда для 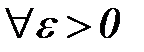 (
(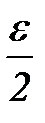 ) при
) при 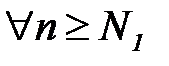 выполняется неравенство:
выполняется неравенство:
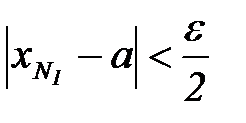 [29].
[29].
Бесконечно малые последовательности
Определение №1. Последовательность 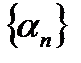 называется бесконечно малой, если она имеет предел, равный 0, т.е.
называется бесконечно малой, если она имеет предел, равный 0, т.е. 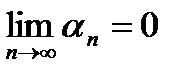 .
.
Определение №2. Последовательность 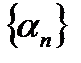 будет бесконечно малой, если
будет бесконечно малой, если 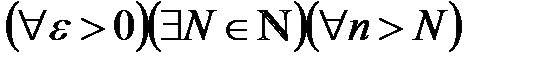 будет выполняться неравенство
будет выполняться неравенство 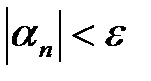 .
.
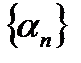 – бмп
– бмп 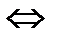
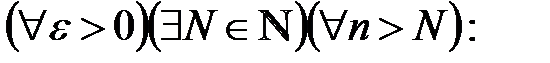
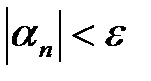 .
.
Замечание. Характерным для бесконечно малой последовательности является то, что она своим пределом имеет 0, а не то насколько малые значения она принимает.
Пример. Дана последовательность 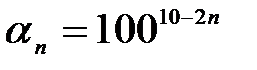 . Она принимает значения: 1008;1006;1004;1002;1;
. Она принимает значения: 1008;1006;1004;1002;1; 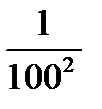 ;
; 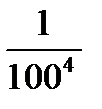 ;
; 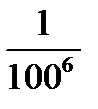 ;
; 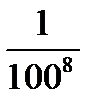 ;…..Эта последовательность является бесконечно малой, так как
;…..Эта последовательность является бесконечно малой, так как 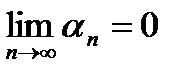 , хотя значения отдельных элементов очень велики.
, хотя значения отдельных элементов очень велики.
Примеры бесконечно малых последовательностей: 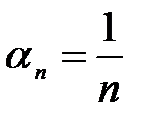 ;
; 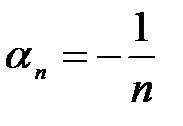 ;
; 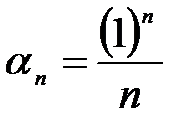 ;
; 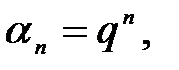
 2020-10-10
2020-10-10 265
265








