2020-10-10
858
Определение №1. Последовательность 
называется возрастающей, если каждый её элемент, начиная со второго, больше предыдущего, т.е. выполняется неравенство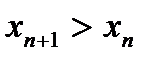 
, 
.
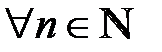Определение №2. Последовательность называется убывающей, если каждый её элемент, начиная со второго, меньше предыдущего, т.е. выполняется неравенство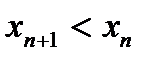 
, 
.
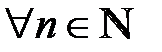Определение №3. Последовательность называется невозрастающей, если каждый её элемент, начиная со второго, не больше предыдущего, т.е. выполняется неравенство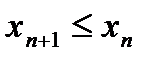 
, .
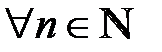Определение№4. Последовательность называется неубывающей, если каждый её элемент, начиная со второго, не меньше предыдущего, т.е. выполняется неравенство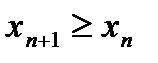 
, .
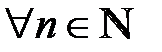Определение №5. Убывающие, возрастающие, неубывающие, невозрастающие последовательности называются монотонными. А возрастающие и убывающие последовательности называются строго монотонными.
Примеры: а)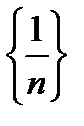 
:1;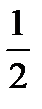 
; 
;…; 
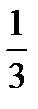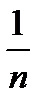;… – убывающая, ограниченная (
, 
).
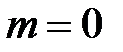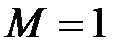б) 1; 1; 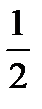; ; 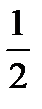; ;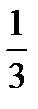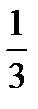…; ; 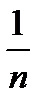;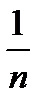… – невозрастающая, ограниченная (
, 
).
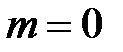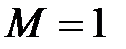в) 1; 2; 3;…; n;… – возрастающая, ограниченная снизу и неограниченная сверху (,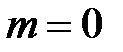 
).
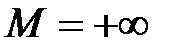г) 1; 1; 2; 2; 3; 3; 4; 4;…; n; n;… – неубывающая, ограниченная снизу и неограниченная сверху (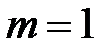
, 
).
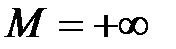д)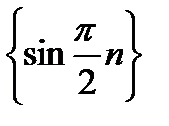 
: 1; 0; -1; 0; 1; 0; -1;… – ограниченная (
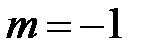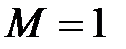, ), не является монотонной.
Замечание: 1.Монотонные последовательности ограниченны, по крайней мере, с одной стороны
а)неубывающие – ограничены снизу, так как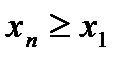 
и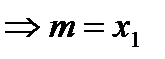 
, ;
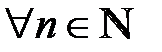б)невозрастающие – ограничены сверху, так как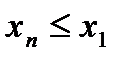 
, 
, 
.
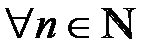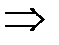
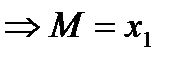2.Если монотонные последовательности ограниченны с обеих сторон, т.е. просто ограничены, то они сходятся.
3.Немонотонные последовательности этим свойством не обладают.
Пример: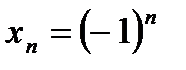 
– ограничена, не является монотонной и не имеет предела.
Карл Теодор Вильгельм Вейерштрасс (1815-1897) – немецкий математик.
Теорема:1. Всякая возрастающая последовательность имеет предел, конечный, если она ограничена сверху и бесконечный предел, равный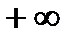 
, если она неограниченна сверху. Причем, предел последовательности равен её точной верхней грани: 
.
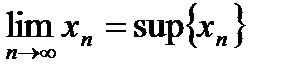2. Всякая убывающая последовательность имеет предел, конечный, если она ограничена снизу, и бесконечный предел, равный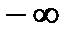 
, если она неограниченна снизу, причем, предел последовательности равен её точной нижней грани: 
.
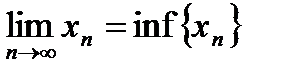Доказательство: I. 1.Пусть последовательность возрастает и ограничена сверху. Требуется доказать, что она сходится и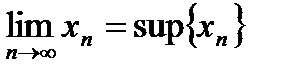 
.
2.Так как последовательность ограничена сверху, то множество значений её элементов ограничено сверху.
3.В соответствии с теоремой: «Всякое ограниченное сверху непустое числовое множество имеет точную верхнюю грань и … т.д.», то последовательность имеет точную верхнюю грань, т.е. пусть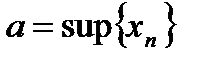 
.
4.На основании свойства точной верхней грани, можно записать:
а) 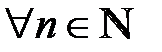выполняется неравенство 
;
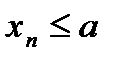б)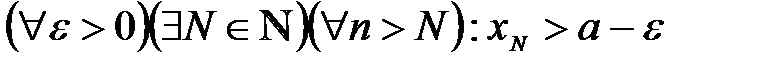 
.
5.Так как последовательность возрастающая, то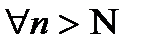 
справедливо 
.
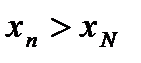6.Рассмотрим неравенства: ;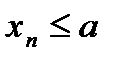 
; : 
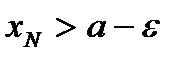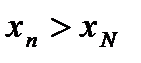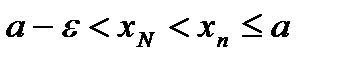или 
, ил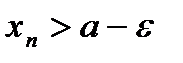и 
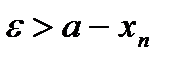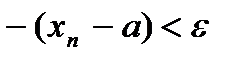, или 
, или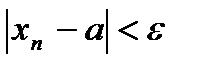 
(так как , 
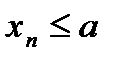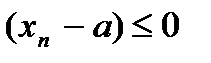с учетом определения модуля, если 
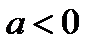, то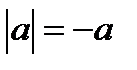 
).
7.Последнее неравенство равносиль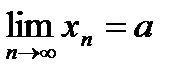но 
, но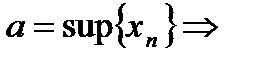 
.
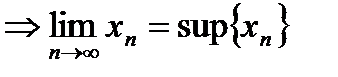Ч.т.д.
Доказательство: II. 1.Пусть последовательность неограниченна сверху и возрастает. Требуется доказать, что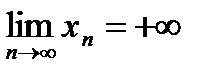 
.
2.Известно, что если множество неограниченно сверху, то пишут
.
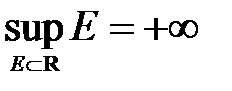3.Значит, и множество значений последовательности, неограниченной сверху, тоже будет иметь такую верхнюю грань: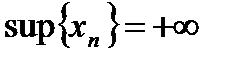 
.
4.Так как последовательность неограниченна сверху, то
.
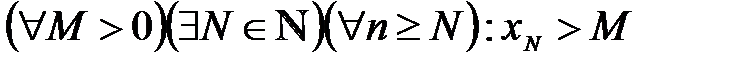5.Так как последовательность возрастающая, то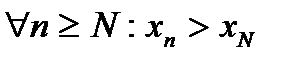 
.
6.Сравним неравенства: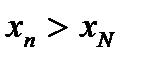 
и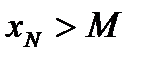 
.
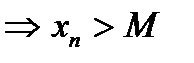7.Последнее неравенство говорит о том, что является бесконечно большой последовательностью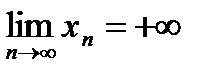 
.
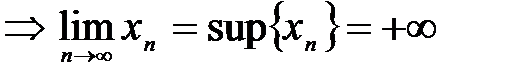Ч.т.д.
Замечание: 1. Аналогично разбирается случай убывающей последовательности.
2. Утверждения теоремы остаются в силе, если последовательность становится монотонной с определенного номера, так как без влияния на предел последовательности можно отбросить любое число её первых элементов.
Следствие №1. Для того, чтобы возрастающая последовательность сходилась необходимо и достаточно, чтобы она была ограничена сверху.
Следствие №2. Для того, чтобы убывающая последовательность сходилась необходимо и достаточно, чтобы она была ограничена снизу.
