Особые случаи к теоремам о пределе суммы

Произведения, частного

Материал будет рассмотрен на практическом занятии №6.

Последовательность ,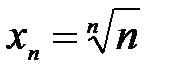

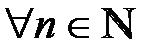
1.Дана последовательность 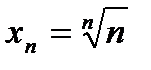. Требуется доказать, что .

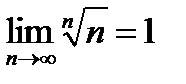2.Согласно лемме, если последовательность  имеет предел 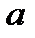, то её общий элемент может быть представлен в виде 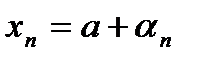, т.е. в данном случае

.

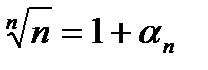Если удастся доказать, что 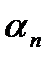  –бесконечно малая последовательность, то докажем, что 1 – предел последовательности .

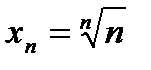3.Очевидно, что 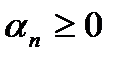 при .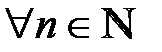

4.Возведем обе части равенства 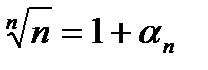  в 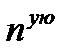  степень: .

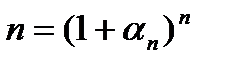5.В соответствии с формулой бинома Ньютона:

.

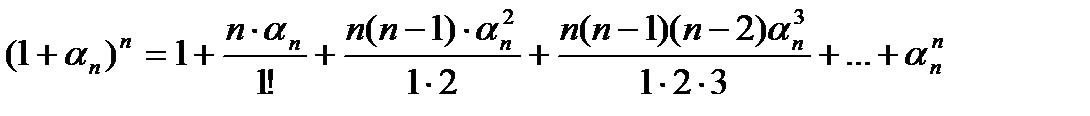6.Все слагаемые, стоящие справа, неотрицательны. Если отбросить все слагаемые, кроме 1^ого и 3^ого, то равенство превратится в неравенство

, .

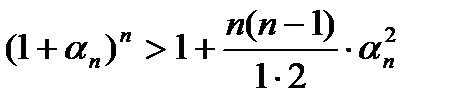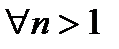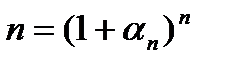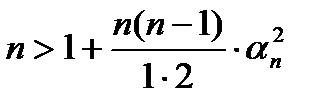7.Так как , то  или .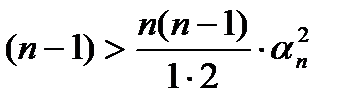

8.Разделим обе части неравенства на положительное число :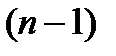

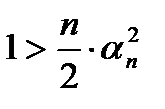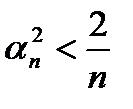 или   или .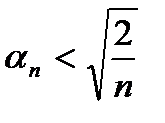

9.Но 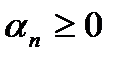, тогда .

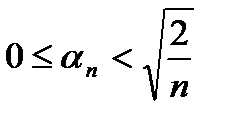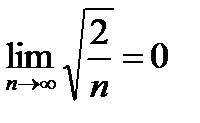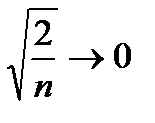10.  т.е.   при 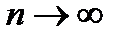. Следовательно,  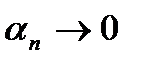при 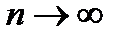  по теореме о сжатой переменной, т.е.  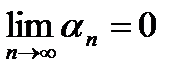 или 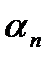  –бесконечно малая последовательность. Значит, 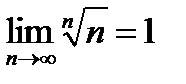, так как выполняется равенство .

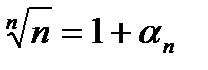Ч.т.д.

Последовательность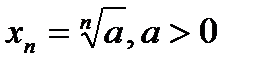

1.Пусть дана последовательность 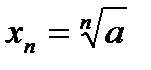. Требуется доказать, что  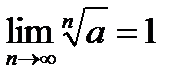 при .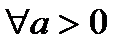

2.Для 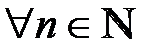, начиная с некоторого номера будет выполняться неравенство 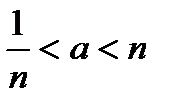, причем  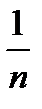– для случая .

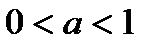3.Извлечем корень n^ой степени из всех положительных частей неравенства

.

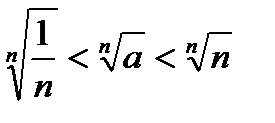4.Известно, что 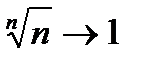  при 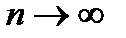. Поэтому .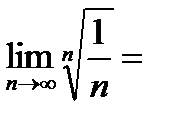

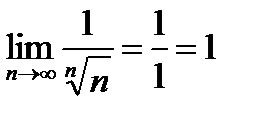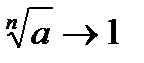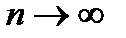5.В соответствии с теоремой о сжатой переменной   при   для 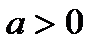, т.е. .

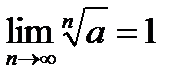Ч.т.д.