Тема №2
Предел последовательности
Лекция №6
1. Последовательность 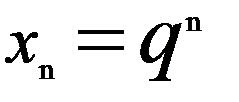 ,
, 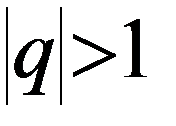 .
.
2. Замечание о бесконечно больших неограниченных последовательностях.
3. Основные теоремы о пределах последовательностей.
4. Особые случаи к теоремам о пределе суммы, произведения и частного.
5. Последовательности 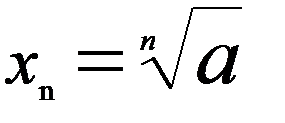 ,
, 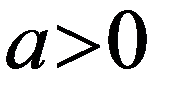 и
и  ,
, 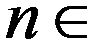 N.
N.
6. Понятие точных граней у последовательностей.
Бесконечно большая последовательность 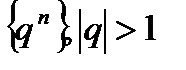
Доказательство провести самостоятельно.
Замечание о бесконечно больших и неограниченных последовательностях.
Очевидно, что любая бесконечно большая последовательность является неограниченной. Однако неограниченная последовательность может и не быть бесконечно большой.
Пример: Неограниченная последовательность 1;2;1;3;1;4;…1;n;… не является бесконечно большой, так как неравенство 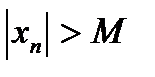 при
при 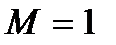 выполняется не для всех элементов
выполняется не для всех элементов 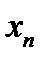 , т.е. для элементов с нечетными номерами не выполняется.
, т.е. для элементов с нечетными номерами не выполняется.
Основные теоремы о пределах последовательностей или свойства пределов, связанные с арифметическими операциями над последовательностями
Лемма: Для того, чтобы число a являлось пределом последовательности  необходимо и достаточно, чтобы её общий элемент
необходимо и достаточно, чтобы её общий элемент  имел вид:
имел вид:
 при
при  , где
, где 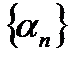 – бесконечно малая последовательность.
– бесконечно малая последовательность.
Доказательство: Необходимость. 1.Пусть дана последовательность  , которая сходится к числу
, которая сходится к числу 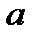 . Надо доказать, что разность
. Надо доказать, что разность  – является бесконечно малой последовательностью.
– является бесконечно малой последовательностью.
2.Так как  сходится к
сходится к 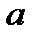 , то на основании определения предела последовательности
, то на основании определения предела последовательности 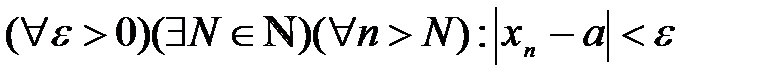 .
.
3.Так как  , то заменим подмодульное выражение:
, то заменим подмодульное выражение: 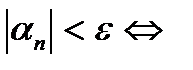

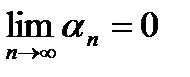 . Значит,
. Значит, 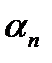 – бесконечно малая последовательность.
– бесконечно малая последовательность.
Ч.т.д.
Достаточность. 1.Общий элемент последовательности имеет вид  , где
, где 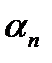 – бесконечно малая последовательность. Требуется доказать, что
– бесконечно малая последовательность. Требуется доказать, что 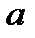 – предел этой последовательности.
– предел этой последовательности.
2.Перепишем формулу  по иному:
по иному:  .
.
3.Найдем модули от обеих частей выражения: 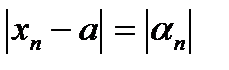 .
.
4.Так как  , то
, то 
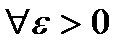 при
при  .
.
5.Неравенство  равносильно равенству
равносильно равенству  , т.е.
, т.е.  сходится к
сходится к 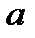 .
.
Ч.т.д.
Замечание:1. Эта лемма показывает особую роль бесконечно малых последовательностей при изучении понятия предела последовательности.
2. Общее понятие предела последовательности сводится с помощью этой леммы к понятию нулевого предела.
3. Это обстоятельство используется при изучении ряда свойств сходящейся последовательности.
Теорема №1: Предел константы есть сама константа, т.е. если 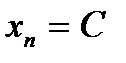 , то
, то 
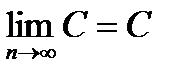 ,
, 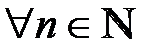 .
.
Доказать самостоятельно.
Теорема №2: Если последовательности  и
и  сходятся, то последовательность
сходятся, то последовательность 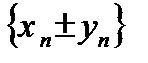 также сходится, и
также сходится, и  , т.е. предел алгебраической суммы двух сходящихся последовательностей равен алгебраической сумме пределов этих последовательностей.
, т.е. предел алгебраической суммы двух сходящихся последовательностей равен алгебраической сумме пределов этих последовательностей.
Доказательство: 1.Пусть последовательности  и
и  сходятся, т.е.
сходятся, т.е.  и
и 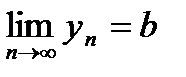 . Доказать, что последовательность
. Доказать, что последовательность 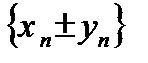 сходится, и
сходится, и  .
.
2.Так как,  ,
, 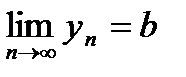 , то в соответствии с леммой можно записать
, то в соответствии с леммой можно записать 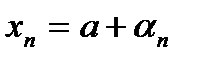 ,
, 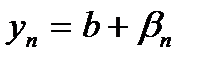 ,
, 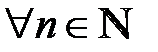 .
.
3.Алгебраическая сумма общих элементов этих последовательностей имеет вид: 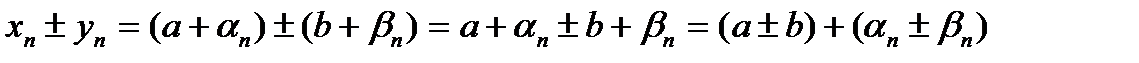 .
.
4.Согласно теореме об алгебраической сумме двух бесконечно малых последовательностей слагаемое  – будет также бесконечно малой последовательностью.
– будет также бесконечно малой последовательностью.
5.Таким образом, последовательность с общим элементом 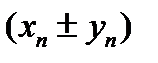 удалось представить в виде суммы конечного числа
удалось представить в виде суммы конечного числа  и бесконечно малой последовательности.
и бесконечно малой последовательности.
6.Тогда согласно лемме о представлении общих элементов последовательности через предел и бесконечно малую последовательность число  является пределом последовательности,
является пределом последовательности, 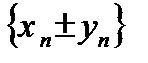 , т.е.
, т.е. 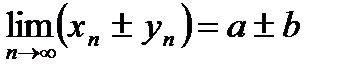 .
.
7.Но 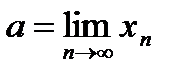 ,
,  поэтому
поэтому  .
.
Ч.т.д.
Следствие к теореме №2: Предел алгебраической суммы конечного числа сходящихся последовательностей равен алгебраической сумме пределов этих последовательностей.
Такое утверждение следует из теоремы №2 и метода математической индукции.
Теорема №3: Если последовательности  и
и  сходятся, то последовательность
сходятся, то последовательность 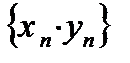 также сходится, и
также сходится, и 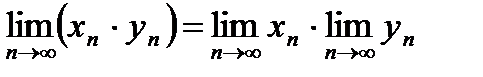 , т.е. предел произведения двух сходящихся последовательностей существует и равен произведению пределов данных последовательностей.
, т.е. предел произведения двух сходящихся последовательностей существует и равен произведению пределов данных последовательностей.
Доказательство: 1.Пусть последовательности  и
и  сходятся, т.е.
сходятся, т.е.  ,
, 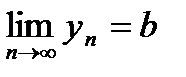 . Требуется доказать, что
. Требуется доказать, что 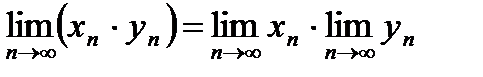 , т.е. что последовательность
, т.е. что последовательность 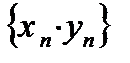 – сходится.
– сходится.
2.Тогда согласно лемме о представлении общего элемента последовательности через предел и бесконечно малые последовательности  и
и  можно представить так
можно представить так 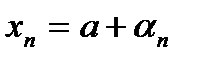 ,
, 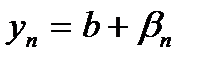 , где
, где 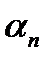 ,
, 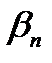 – бесконечно малые последовательности, т.е.,
– бесконечно малые последовательности, т.е., 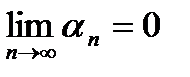 ,
, 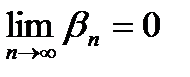 .
.
3.Произведение общих элементов этих последовательностей примет вид 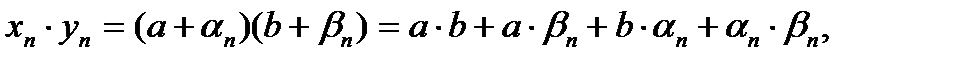 где
где  и
и 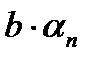 – есть произведение постоянной величины на бесконечно малую последовательность.
– есть произведение постоянной величины на бесконечно малую последовательность.
Постоянная величина может быть рассмотрена как частный случай ограниченной последовательности. Следовательно, 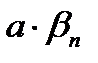 и
и 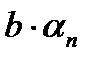 будут бесконечно малыми последовательностями.
будут бесконечно малыми последовательностями. 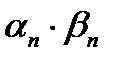 – это произведение двух бесконечно малых последовательностей. В соответствии с теоремой о произведении двух бесконечно малых последовательностей это выражение будет бесконечно малой последовательностью.
– это произведение двух бесконечно малых последовательностей. В соответствии с теоремой о произведении двух бесконечно малых последовательностей это выражение будет бесконечно малой последовательностью. 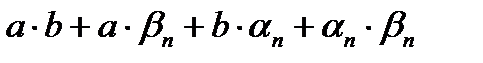 – бесконечно малая последовательность на основании теоремы об алгебраической сумме бесконечно малых последовательностей.
– бесконечно малая последовательность на основании теоремы об алгебраической сумме бесконечно малых последовательностей.
4.Итак, произведение 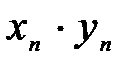 представимо в виде конечного числа
представимо в виде конечного числа  и бесконечно малой последовательности. Следовательно, число
и бесконечно малой последовательности. Следовательно, число  можно считать пределом последовательности
можно считать пределом последовательности 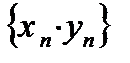 в соответствии с леммой, т.е.
в соответствии с леммой, т.е.
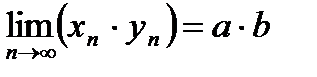 , но
, но 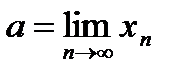 ,
, 
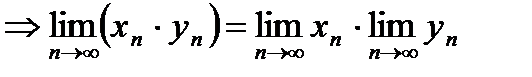 .
.
Ч.т.д.
Следствие №1 к теореме №3. Если  сходится, то для любого числа
сходится, то для любого числа  , где
, где 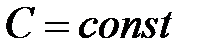 ,
,  , последовательность
, последовательность 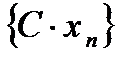 также сходится, причем
также сходится, причем
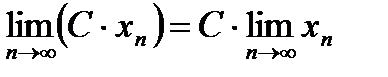 , т.е. постоянную можно выносить за знак предела.
, т.е. постоянную можно выносить за знак предела.
Данное утверждение следует из теоремы №3 и теоремы №1.
Следствие №2 к теореме №3. Если  – сходящаяся последовательность и
– сходящаяся последовательность и  , то
, то  . Предел степени есть степень предела.
. Предел степени есть степень предела.
Это утверждение следует из теоремы №3 и метода математической индукции.
Теорема №4: Если последовательности  и
и  сходятся и
сходятся и 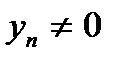 ,
,  ,
,  , то последовательность
, то последовательность 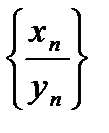 сходится и
сходится и 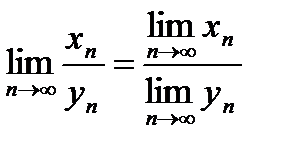 (т.е. при сделанных допущениях предел частного двух сходящихся последовательностей равен частному от пределов данных последовательностей).
(т.е. при сделанных допущениях предел частного двух сходящихся последовательностей равен частному от пределов данных последовательностей).
Доказательство: 1.Пусть  ,
,  – сходятся, т.е.
– сходятся, т.е.  ,
, 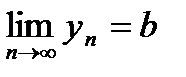 . Требуется доказать, что
. Требуется доказать, что 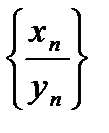 сходится, когда
сходится, когда 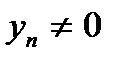 ,
,  ,
,  и
и
справедлива формула 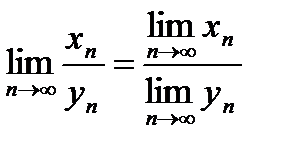 .
.
2.Так как  ,
,  – сходятся, то в соответствии с леммой можно написать
– сходятся, то в соответствии с леммой можно написать 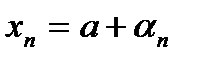 ,
, 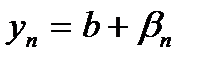 , где
, где 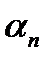 ,
, 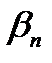 – бесконечно малые последовательности.
– бесконечно малые последовательности.
3.Перепишем выражение п.2 по другому  ,
, 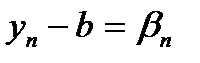 .
.
4.Тогда для доказательства теоремы №4 достаточно показать, что  – бесконечно малая последовательность.
– бесконечно малая последовательность.
5.Приведем к общему знаменателю это выражение:


где 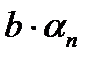 ;
; 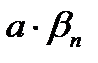 – есть произведение постоянной величины на бесконечно малую последовательность, а значит, есть бесконечно малая последовательность.
– есть произведение постоянной величины на бесконечно малую последовательность, а значит, есть бесконечно малая последовательность.
Тогда разность двух бесконечно малых последовательностей (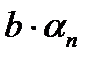
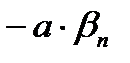 ) – тоже бесконечно малая последовательность в соответствии с теоремой об алгебраической сумме двух бесконечно малых последовательностей.
) – тоже бесконечно малая последовательность в соответствии с теоремой об алгебраической сумме двух бесконечно малых последовательностей.
6.Остается показать, что величина 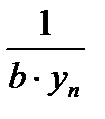 есть ограниченная последовательность. Тогда произведение ограниченной на бесконечно малую последовательность даст бесконечно малую последовательность. И теорема будет доказана.
есть ограниченная последовательность. Тогда произведение ограниченной на бесконечно малую последовательность даст бесконечно малую последовательность. И теорема будет доказана.
7.Так как 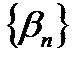 – бесконечно малая последовательность, то на основании определения бесконечно малой последовательности можно записать
– бесконечно малая последовательность, то на основании определения бесконечно малой последовательности можно записать
 .
.
8.Последовательность  согласно лемме представима так:
согласно лемме представима так:  .
.
9.Найдем модуль от обеих частей этого равенства: 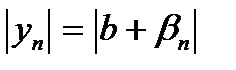 .
.
10.По свойству модуля суммы двух действительных чисел  , можно записать
, можно записать 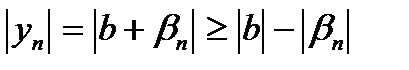 .
.
11.Подставим в правую часть неравенства вместо 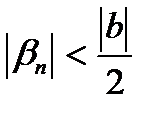 , тем самым уменьшим правую часть, увеличив вероятность выполнения неравенства.
, тем самым уменьшим правую часть, увеличив вероятность выполнения неравенства.
 или
или 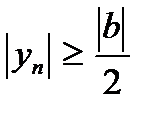 , т.е.
, т.е. 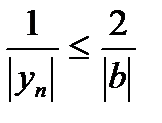 .
.
12.По свойству модуля частного действительных чисел 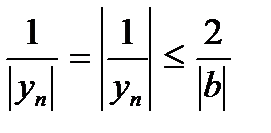 .
.
13.Умножим обе части неравенства на положительное число 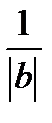 , получим
, получим
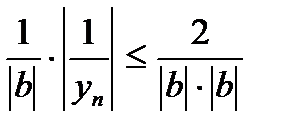 или
или  .
.
Если в качестве  , то последнее неравенство говорит о том, что последовательность
, то последнее неравенство говорит о том, что последовательность 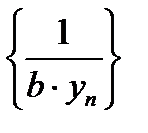 – ограниченная.
– ограниченная.
14.Следовательно, 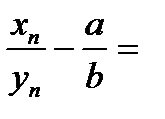
 – есть бесконечно малая последовательность.
– есть бесконечно малая последовательность.
Значит, последовательность  имеет предел
имеет предел  , т.е.
, т.е. 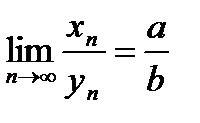 , но
, но 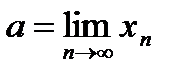 ,
,  , то
, то 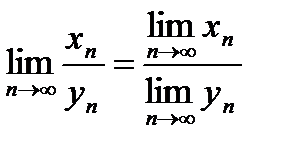 при
при 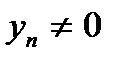 ,
,  ,
, 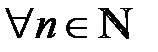 .
.
Ч.т.д.
Замечание: Если последовательности имеют бесконечные пределы, то в общем случае утверждения теорем неверны.
 2020-10-10
2020-10-10 340
340







