Десятичной дробью
Лемма: Каково бы ни было действительное число  , последовательность
, последовательность  монотонно убывает, последовательность
монотонно убывает, последовательность 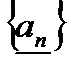 монотонно возрастает, и
монотонно возрастает, и 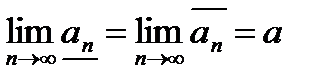 .
.
Доказательство: 1.Пусть задано некоторое действительное число  . Для определенности, пусть
. Для определенности, пусть 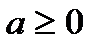 .
.
2.В силу аксиомы Архимеда: «Каково бы ни было число, существует такое натуральное число  , что,
, что, 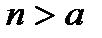 : (
: ( )(
)(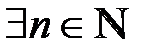 ):
): 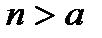 ».
».
3.Среди натуральных чисел 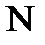 возьмем такое
возьмем такое 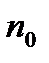 , наименьшее из них и обладающее свойством
, наименьшее из них и обладающее свойством 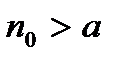 . Обозначим его
. Обозначим его 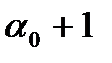 , т.е.
, т.е. 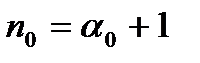 .
.
4.Так как 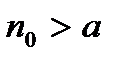 , то
, то 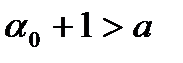 . Значит, можно написать
. Значит, можно написать 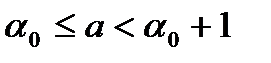 .
.
Покажем на рисунке.

5.Обозначим отрезок 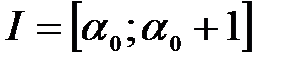 и разобьем его на 10 равных частей.
и разобьем его на 10 равных частей.

6.Рассмотрим последовательность отрезков  , где
, где 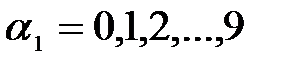 .
.
1ый отрезок будет 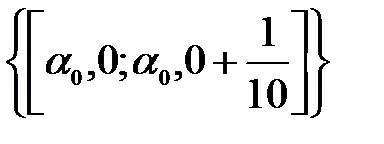 =
= 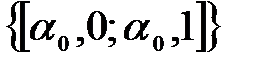 , когда
, когда 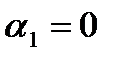
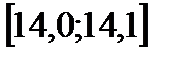 .
.
2ой отрезок будет 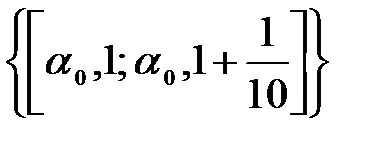 =
= 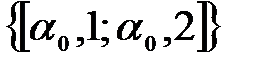 , когда
, когда 
 .
.
………………………………………………………
10ый отрезок будет  =
= 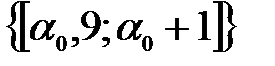 , когда
, когда 
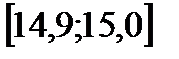 .
.
7.Для точки 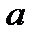 возможны два случая:
возможны два случая:
а) либо точка 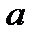 не совпадает ни с одной точкой деления;
не совпадает ни с одной точкой деления;
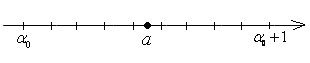
б) либо точка 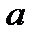 совпадает с одной из точек деления
совпадает с одной из точек деления

или

8.В случае а) точка 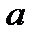 принадлежит только одному отрезку. Обозначим его
принадлежит только одному отрезку. Обозначим его 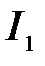 ;
;  :
: 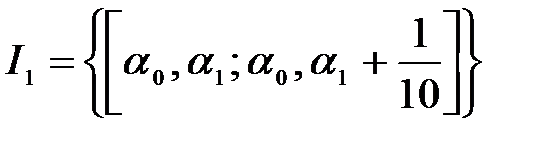 , где
, где  .
.
9.В другом случае точка 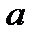 принадлежит сразу двум отрезкам. Тогда через
принадлежит сразу двум отрезкам. Тогда через 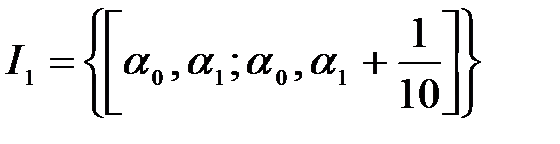 обозначим из них тот, для которого точка
обозначим из них тот, для которого точка 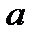 не является правым концом,
не является правым концом,  .
.
10.Разобьем отрезок  в свою очередь на десять равных частей, на 10 равных отрезков.
в свою очередь на десять равных частей, на 10 равных отрезков.
11.Обозначим через 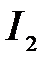 тот из них, который содержит точку
тот из них, который содержит точку 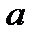 , и для которого точка
, и для которого точка 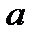 не является правым концом
не является правым концом 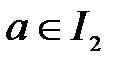 .
.
12.Продолжая этот процесс разбиения на отрезок, получим последовательность вложенных отрезков:  , где
, где 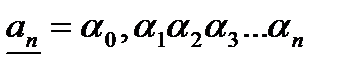 ,
,  (
(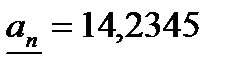 ,
, 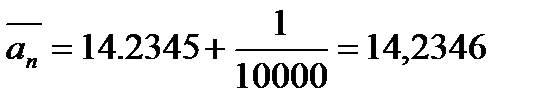 ).
).
13.Каждый из отрезков содержит точку 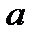 , причем точка
, причем точка 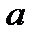 не является его правым концом
не является его правым концом 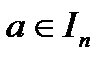
 ,
, 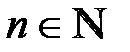 .
.
14.Длина nого отрезка 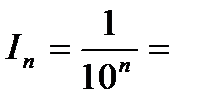


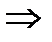
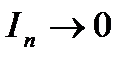 при
при 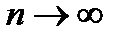 .
.
Определение №1: Конечные десятичные дроби  ,
, 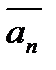 называются десятичными дробями, приближающими число
называются десятичными дробями, приближающими число 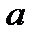 .
.
Определение №2: Число 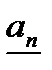 называется нижним десятичным приближением порядка
называется нижним десятичным приближением порядка  числа
числа 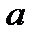 , а число
, а число 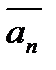 называется верхним десятичным приближением порядка
называется верхним десятичным приближением порядка  числа
числа 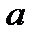 .
.
15.Сформулируем свойства нижнего и верхнего десятичных приближений порядка nого числа 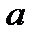 :
:
а) последовательность отрезков 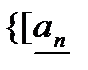 ,
, 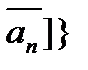 образуют последовательность вложенных отрезков
образуют последовательность вложенных отрезков 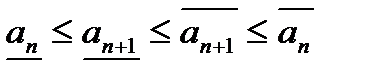 или
или  ;
;
б) длина nого отрезка 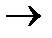 к 0
к 0 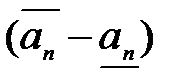
 при
при 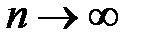
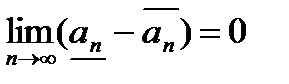 и
и 

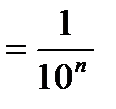 ;
;
в) точка 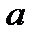 принадлежит всем этим отрезкам
принадлежит всем этим отрезкам 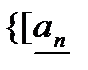 ,
, 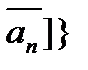 , т.е.
, т.е.
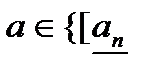 ,
, 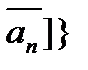 и
и 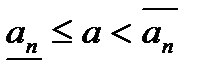 при
при  .
.
г) левые концы отрезков 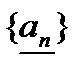 образуют возрастающую последовательность;
образуют возрастающую последовательность;
д) правых концы отрезков образуют убывающую последовательность 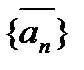 .
.

Следовательно, получаем стягивающую последовательность вложенных отрезков  ,
, 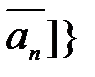 .
.
16.Согласно замечанию №1 к теореме (принципу) Коши-Кантора точка 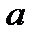 является пределом для последовательностей
является пределом для последовательностей 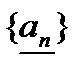 и
и 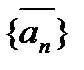 , т.е.
, т.е.
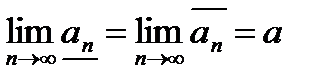 .
.
17.Таким образом, лемма доказана.
Замечание: Если  отрицательно, т.е.,
отрицательно, т.е.,  , то нужно принять
, то нужно принять 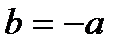 и выполнить подобные исследования.
и выполнить подобные исследования.
Следствие к лемме: Всякое действительное число является пределом последовательности рациональных чисел.
Следствие теоремы вытекает из того, что 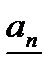 и
и  суть рациональные числа.
суть рациональные числа.
Модуль
Тема №2
 2020-10-10
2020-10-10 182
182








