Лекция №8
1. Число е.
2. Подпоследовательности.
3. Теорема о сходимости подпоследовательности сходящейся последовательности.
4. Теорема Больцано – Вейерштрасса.
Число е
Докажем, что 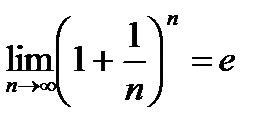 .
.
Доказательство: 1.Рассмотрим последовательность 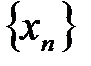 с общим членом
с общим членом  :
:  ,
, 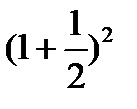 , …,
, …, 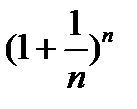 ,…. (2; 2,25; 2,357; 2,44; …,
,…. (2; 2,25; 2,357; 2,44; …,  ,…).
,…).
Требуется доказать, что, 
 – иррациональное число, т.е., что последовательность
– иррациональное число, т.е., что последовательность  сходится к
сходится к  при
при 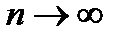 .
.
2.Известно, что возрастающая последовательность, ограниченная сверху сходится к конечному числу.
3.Воспользуемся формулой бинома Ньютона:
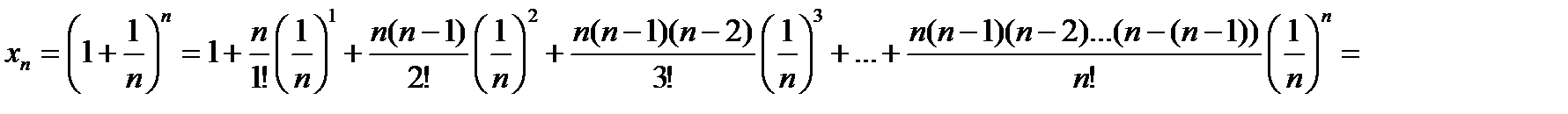
 .
.
4.Представим выражение в следующем виде:
 или
или
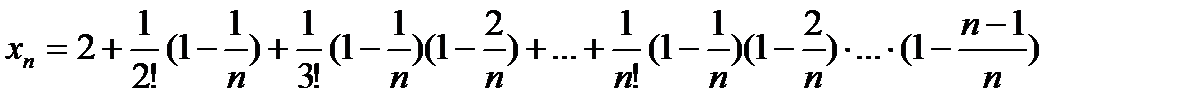 .
.
5.Аналогичным образом представим элемент  данной последовательности:
данной последовательности:
 .
.
6.Сравним два выражения  и
и 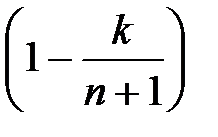 ,
, 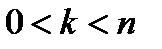 .
.
7.Так как,  , то
, то 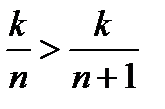 поэтому
поэтому 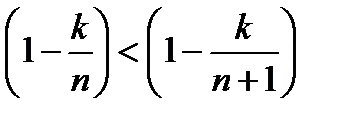 .
.
8.Сравним 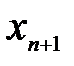 и
и 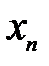 .
.
Каждое слагаемое в выражении  больше соответствующего слагаемого в выражении
больше соответствующего слагаемого в выражении  . Кроме того, у
. Кроме того, у  по сравнению с
по сравнению с  добавляется одно положительное слагаемое. Следовательно,
добавляется одно положительное слагаемое. Следовательно, 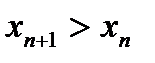 , т.е. последовательность
, т.е. последовательность  возрастает. Осталось доказать, что она ограничена сверху.
возрастает. Осталось доказать, что она ограничена сверху.
9.Рассмотрим опять nый элемент последовательности:
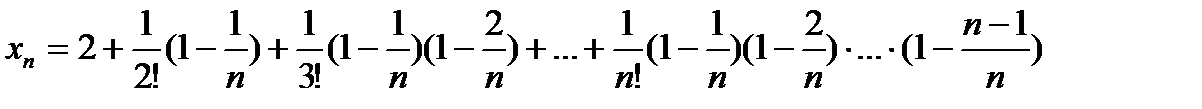 .
.
10.Каждое выражение, стоящее в круглых скобках меньше 1, т.е.
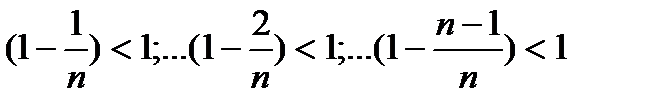 .
.
11.Учитывая это, получим, 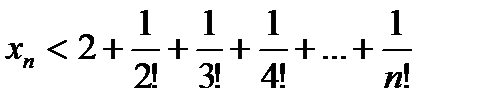 , так как
, так как

 .
.
12.Известно, что  при
при  .
.
(Например,  ;
;  и т.д.).
и т.д.).
13.Поэтому можно записать  или
или  .
.
14.Но 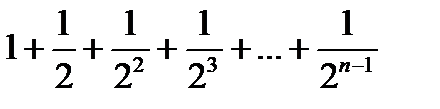 это сумма убывающей геометрической прогрессии с
это сумма убывающей геометрической прогрессии с  ;
;  . Следовательно,
. Следовательно,  .
.
15.Тогда 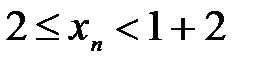 или
или  при
при 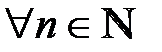 .
.
16.Итак, последовательность 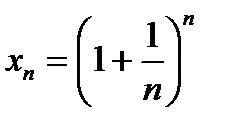 возрастает и ограничена сверху 3.
возрастает и ограничена сверху 3.
А всякая последовательность, возрастающая и ограниченная сверху (по теореме Вейерштрасса) имеет конечный предел. Как оказалось
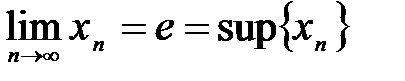 .
.
Ч.т.д.
Модуль
Тема №3
Функции и их свойства. Операции над функциями. Композиция функций. Обратная функция. Предел функции
Лекция №9
1. Понятие функции.
2. Операции над функциями.
3. Ограниченные сверху, снизу и ограниченные функции.
4. Наибольшее, наименьшее, максимальные, минимальные и экстремальные значения функции.
5. График функции.
6. Способы задания функции. Композиция функций.
7. Классификация функций.
8. Четные, нечетные функции и их свойства.
9. Периодические функции.
Понятие функции
Определение. Пусть  и
и 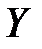 – некоторые числовые множества. Функцией называется множество
– некоторые числовые множества. Функцией называется множество 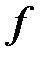 упорядоченных пар чисел
упорядоченных пар чисел  таких, что
таких, что 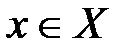 ,
,  , а каждое
, а каждое  входит в одну и только в одну пару такого множества
входит в одну и только в одну пару такого множества 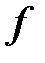 , а каждое y входит, по крайней мере, в одну пару этого множества
, а каждое y входит, по крайней мере, в одну пару этого множества 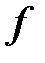 .
.
При этом говорят, что числу  поставлено в соответствие число
поставлено в соответствие число 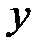 и пишут:
и пишут:  . Число
. Число 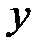 называется значением функции
называется значением функции 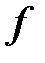 в точке
в точке  . Переменную
. Переменную 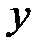 называют зависимой переменной, а переменную
называют зависимой переменной, а переменную  называют независимой переменной или аргументом.
называют независимой переменной или аргументом.
Множество  называют областью определения (или существования) функции
называют областью определения (или существования) функции 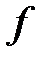 , а множество
, а множество 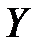 – множеством значения функции
– множеством значения функции 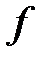 .
.
Замечание. 1. Кроме буквы 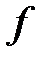 для обозначения функции используют и другие буквы:
для обозначения функции используют и другие буквы: 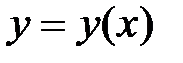 ;
;  ;
; 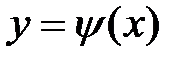 ;
; 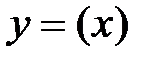 .
.
2. Другими буквами может быть обозначена и зависимая, и независимая переменные.
3. Наряду с термином «функция» употребляют равнозначные термин «отображение». Говорят, что отображение 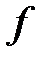 отображает число
отображает число 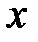 в число
в число 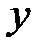 или что число
или что число 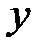 является образом числа
является образом числа 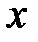 при отображении
при отображении 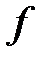 .
.
 2020-10-10
2020-10-10 327
327








