2020-10-10
1367
(принцип стягивающихся отрезков)
Георг Кантор (1845-1918) – немецкий математик.
Этот принцип может быть положен в основу построения действительных чисел в качестве аксиомы непрерывности или полноты.
Определение: Пусть дана последовательность отрезков 
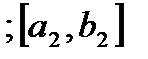
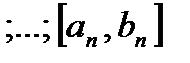
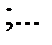таких, что последующий отрезок содержится в предыдущем: 
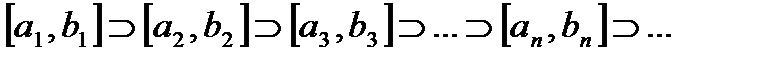, т.е. отрезок 
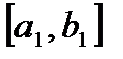содержит отрезок 
, отрезок содержит отрезок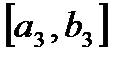 
, и т.д., и выполняется неравенство: 
, 
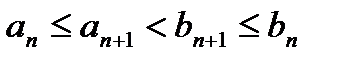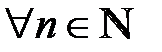. При возрастании 
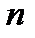длина 
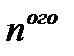отрезка 
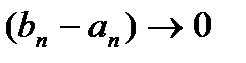, т.е. 
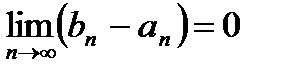. Такая последовательность вложенных отрезков, называется стягивающейся.
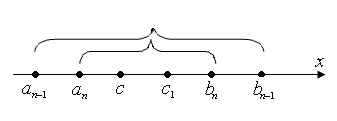
Теорема: Для любой стягивающейся последовательности вложенных отрезков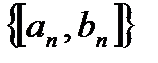 
существует единственная точка c, принадлежащая всем отрезкам этой последовательности, т.е. такая, что 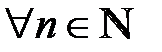справедливо неравенство: 
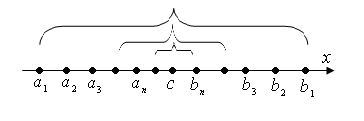
Доказательство:I. 1.Пусть дана стягивающаяся последовательность вложенных отрезков 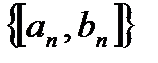. Требуется доказать, что 
, .
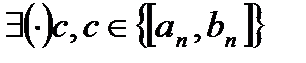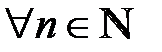2.Левые концы отрезков последовательности 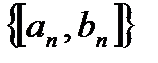образуют монотонную неубывающую последовательность 
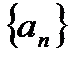, так как по определению 
: 
.
3.Правые концы последовательности 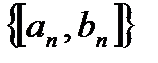образуют монотонную невозрастающую последовательность 
, так как по определению 
, : 
.
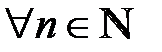4.Последовательность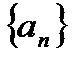 
ограничена сверху, так как , 
.
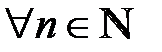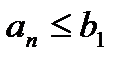5.Последовательность ограничена снизу, так как ,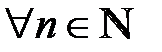 
.
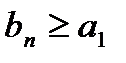6.На основании теоремы Вейерштрасса последовательност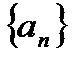и и будут иметь конечные пределы: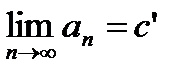 
, 
.
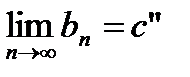7.Так как длина 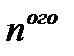отрезка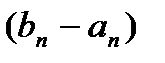 
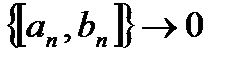при 
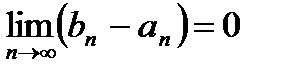, то можно записать или 
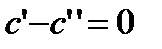или 
или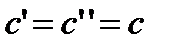 
, т.е. 
.
Значит, последовательност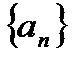и и имеют один и тот же предел c.
8.Так как :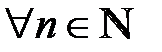 
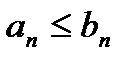, то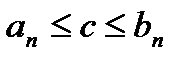 
, т.е. точка c принадлежит всем отрезкам последовательности 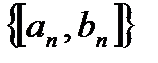. Говорят, что последовательность вложенных отрезков 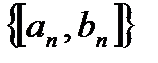стягивается к точке c.
II. 1.Докажем, что точка c – единственна.
2.Доказательство проведем методом от противного, т.е. пусть 
ещё одна точка c1: 
, 
, .
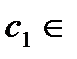
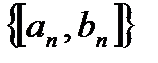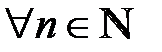3.Тогда для 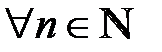должно выполняться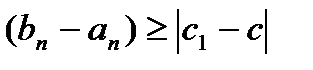 
4.Следовательно,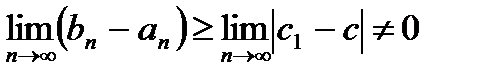 
. А это противоречит условию теоремы. Значит, 
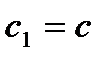. Иточка 
–единственная, принадлежащая всем отрезкам последовательности .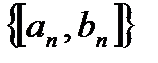
Замечание №1. Если 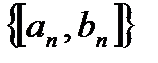– стягивающаяся последовательность вложенных отрезков, и точка 
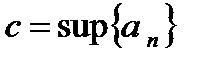–точка, принадлежащая всем отрезкам данной последовательности, то и 
и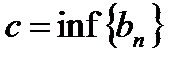 
и последовательность 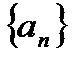– неубывающая, а последовательность – невозрастающая.
Замечание №2. Теорема неверна, если вместо отрезков рассматриваются интервалы.
Пример. Дан интервал (0,1). Разделим его пополам и выберем в качестве
второго интервала его левую половину: 
. Делим интервал снова пополам. И вновь выберем левую половину, т.е.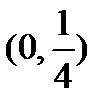 
и т.д. Этот процесс деления и выбора интервалов бесконечный. Следовательно, получается бесконечная последовательность вложенных интервалов: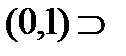 
… 
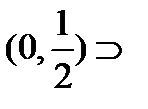
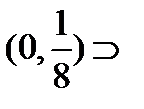. Интервал (0,1) содержит интервал . Интервал содержит интервал 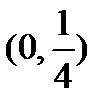и т.д.
Интервалы последовательности 
не имеют ни одной общей точки, так как какую бы мы точку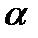 
на промежутке (0,1) ни взяли, найдется такой номер N, что 
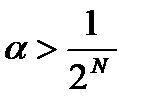. А 
интервалы, начиная с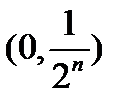 
, не содержат точку 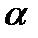. Точка 0 является общим левым концом всех интервалов, но “0”не принадлежит им.
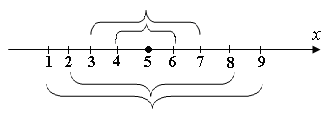
Примеры. а)Построить последовательности вложенных отрезков, стягивающихся к точке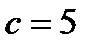 
и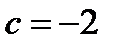 
.
1) 
… 
.
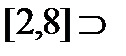
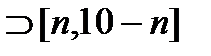
2) 
… 
.
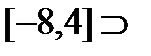
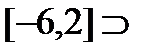
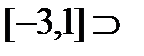
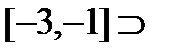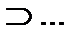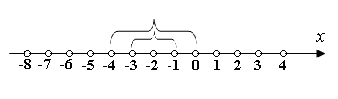
б)К какой точке стягивается последовательность вложенных отрезков
; 
; 
;…; 
;…?
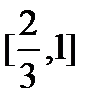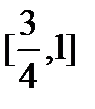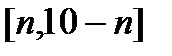Ответ: с=1.
в) Какая последовательность называется вложенной? Стягивающейся?
г) Является ли вложенной последовательность отрезков
; 
;…; 
;…?
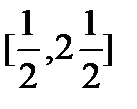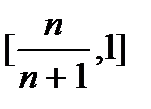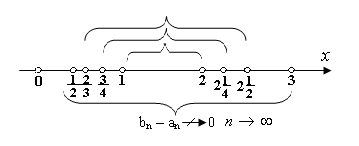
Последовательность вложенных отрезков, но не стягивающаяся, так как стягивается ни к нулю, а к 1 или 2.
д) Является ли вложенной последовательность отрезков
; 
; 
;…; 
;…?
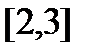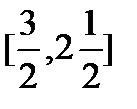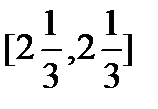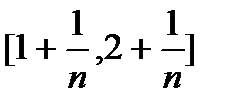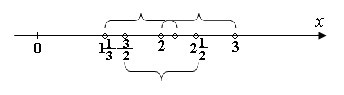
Нет.
е) Отрезок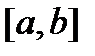 
делится пополам. И берется его левая половина. Потом её делят пополам и берут правую половину. Потом эту половину делят пополам и берут левую половину. Найти общую точку получившихся отрезков.
