Понятие точных граней у последовательностей

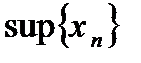Определение №1: Верхняя грань множества значений элементов последовательности  называется верхней гранью данной последовательности и обозначается  или .

 Если верхняя грань является числом, то определение №1 можно сформулировать следующим образом:

Определение №2: Число 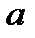 является верхней гранью последовательности , , если

а) для  выполняется неравенство ;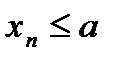

б) для , .

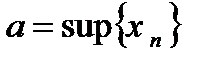Определение №3: Нижняя грань множества значений элементов последовательности  называется нижней гранью данной последовательности  и

обозначается  или .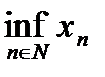

Если нижняя грань является конечным числом, то определение можно сформулировать следующим образом:

Определение №4: Число  является нижней гранью последовательности ,если

а) 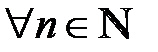 выполняется неравенство ;

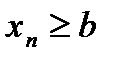б) если , .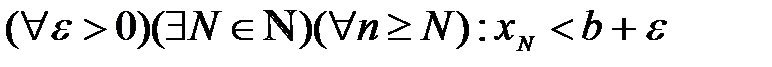

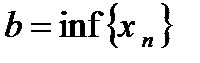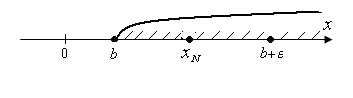
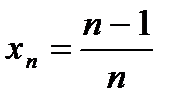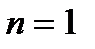
Примеры: 1.  при   ; при   .

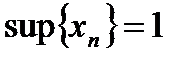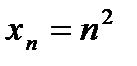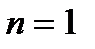
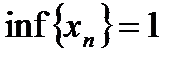2.  при   ; при   .

Модуль

Тема №2

Предел последовательности

Лекция №7

1. Монотонные последовательности.

2. Теорема Вейерштрасса.

3. Принцип вложенных (стягивающихся) отрезков (принцип Коши - Кантора).

4. Замечание о вложенных и только стягивающихся отрезках.

5. Представление действительного числа бесконечной десятичной дробью.