Генрих Эдуард Гейне (1821-1881)– немецкий математик.
1.Пусть дана функция 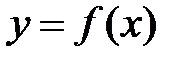 , определённая на некотором множестве
, определённая на некотором множестве 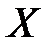 . И пусть точка
. И пусть точка 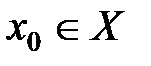 или
или 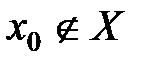 . Возьмём из множества
. Возьмём из множества 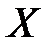 после- довательность точек
после- довательность точек  отличных от
отличных от 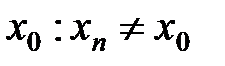 при
при 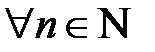 :
:
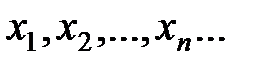 , сходящуюся к
, сходящуюся к 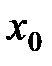 , т.е.
, т.е. 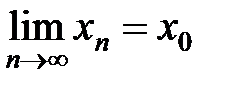 .
.
Таким образом,  — последовательность значений аргумента х. Зна- чения функции в точках этой последовательности также образуют числовую последовательность:
— последовательность значений аргумента х. Зна- чения функции в точках этой последовательности также образуют числовую последовательность: 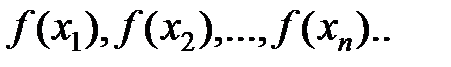 ., т.е.
., т.е. 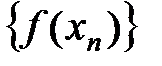 [30].
[30].
Теперь можно поставить вопрос о существовании предела функции 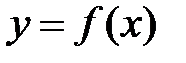 в точке
в точке 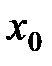 .
.
Определение №1 по Гейне(«на языке последовательностей»). Число 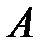 называется пределом функции
называется пределом функции 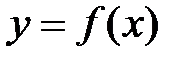 в точке
в точке 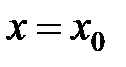 , если для любой сходящейся к
, если для любой сходящейся к 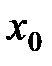 последовательности значений аргумента
последовательности значений аргумента  , отличных от
, отличных от 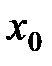 , соответствующая последовательность значений функции
, соответствующая последовательность значений функции 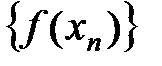 схо- дится к числу
схо- дится к числу 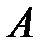 .
.
Символически это записывается так: 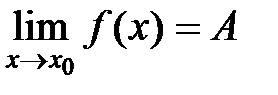 или
или 
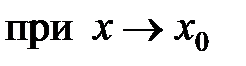 .
.
Из определения следует, что функция 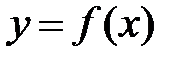 , определенная на множестве Х, имеет предел, равный
, определенная на множестве Х, имеет предел, равный 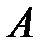 , т.е.
, т.е. 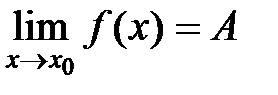 , если
, если
а) 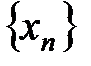 — сходящаяся к
— сходящаяся к 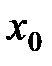 последовательность значений аргумента; причем
последовательность значений аргумента; причем 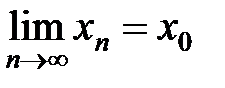 ,
, 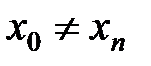 ,
, 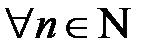 .
.
б) 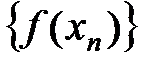 — сходящаяся к
— сходящаяся к 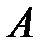 последовательность значений функции, т.е.
последовательность значений функции, т.е. 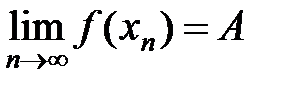 .
.
Примеры. 1). Функция  . Доказать, что эта функция имеет в каждой точке
. Доказать, что эта функция имеет в каждой точке 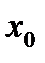 числовой прямой предел, равный
числовой прямой предел, равный  .
.
Доказательство
1. Если 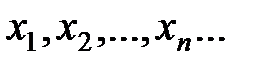 ,
, 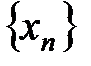 , сходящаяся к
, сходящаяся к 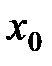 последовательность значений аргумента
последовательность значений аргумента 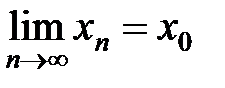 , то последовательность значений функции
, то последовательность значений функции 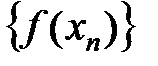 будет иметь вид:
будет иметь вид: 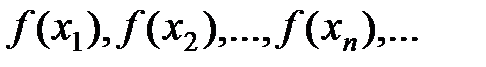 или
или 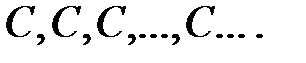
2. Значит, предел последовательности значений функции имеет тот же предел:  .
.
3. На основании определения предела функции в точке по Гейне функция 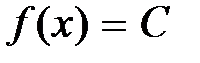 будет иметь тот же предел в точке
будет иметь тот же предел в точке 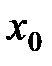 :
: 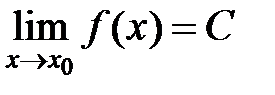 .
.
4. Так как точка 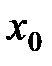 выбиралась произвольно, то функция
выбиралась произвольно, то функция 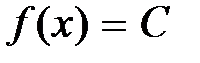 будет иметь в любой точке числовой прямой предел, равный С [30]. Ч.т.д.
будет иметь в любой точке числовой прямой предел, равный С [30]. Ч.т.д.

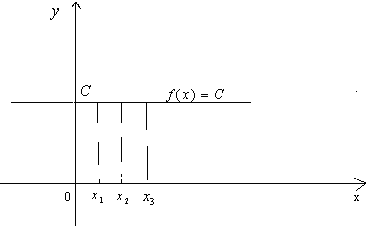
Рис.1.
2). Функция 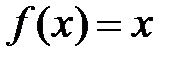 . Доказать, что в каждой точке
. Доказать, что в каждой точке 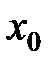 числовой прямой эта функция имеет предел, равный
числовой прямой эта функция имеет предел, равный 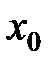 , т.е.
, т.е. 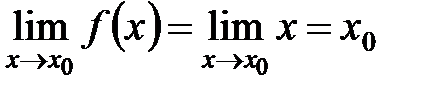 .
. 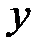
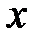
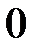
Доказательство
1. Пусть последовательность значений аргумента, сходящаяся к 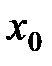 , имеет вид:
, имеет вид: 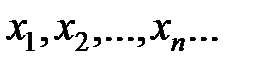 ,
, 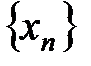 и
и 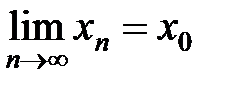 .
.
2. Тогда последовательность значений функции будет иметь вид:
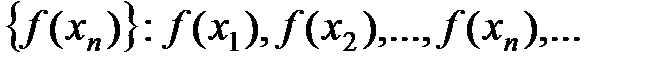 или
или 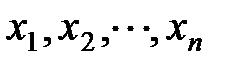 ,…
,… 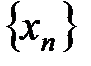 .
.
3. Т. е. последовательности 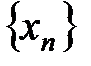 и
и 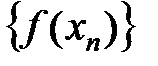 тождественны.
тождественны.
4. Значит, последовательность значений функции имеет тот же предел: 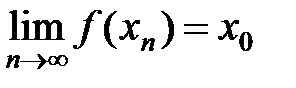
5. Поэтому на основании определения предела функции в точке по Гей- не функция 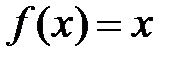 будет иметь тот же предел
будет иметь тот же предел 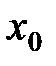 , т. е.
, т. е. 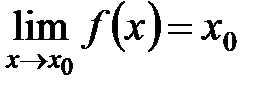 .
.
6. Так как точка 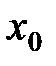 выбиралась произвольно, то функция
выбиралась произвольно, то функция 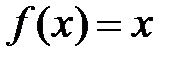 в лю -бой точке
в лю -бой точке 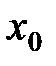 числовой прямой будет иметь предел, равный
числовой прямой будет иметь предел, равный 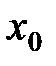 [28]. Ч.т.д.
[28]. Ч.т.д.
3). Функция Дирихле 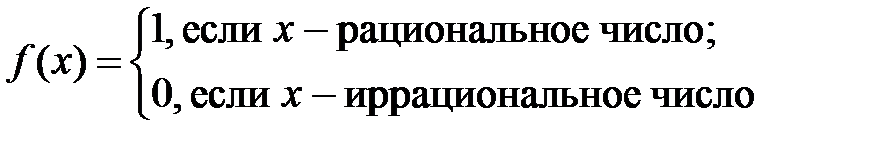 не имеет предела ни в одной точке
не имеет предела ни в одной точке 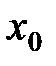 числовой прямой.
числовой прямой.
Доказательство
1. Так для последовательности рациональных значений аргумента, схо- дящейся к 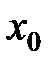 , соответствующая последовательность значений функции имеет предел, равный 1.
, соответствующая последовательность значений функции имеет предел, равный 1.
2. А для последовательности иррациональных значений аргумента, сходящейся к 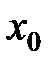 , соответствующая последовательность значений функции будет иметь предел, равный 0.
, соответствующая последовательность значений функции будет иметь предел, равный 0.
3. Следовательно, 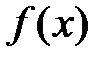 предела не имеет [30]. Ч.т.д.
предела не имеет [30]. Ч.т.д.
Огюстен Луи Коши (1789-1857) –французский математик.
Определение №2 по Коши («на языке 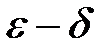 »). Число
»). Число 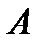 называется пределом функции
называется пределом функции 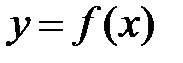 в точке
в точке 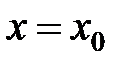 , если для
, если для 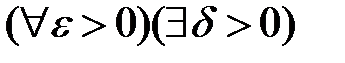
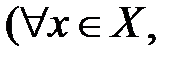
 выполняется неравенство
выполняется неравенство 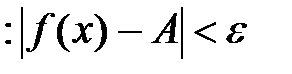 .
.
С помощью символов определение можно записать так:
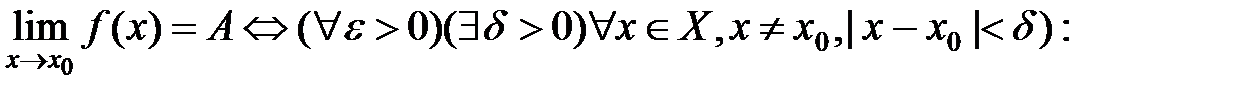
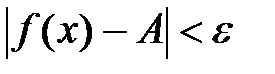 .
.
Замечание №1. Неравенство  можно записать так:
можно записать так:
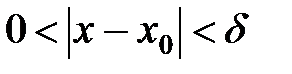 .
.
 2020-10-10
2020-10-10 492
492








