IV. Графический способ задания функции

Соответствие между переменными 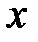 и y задается посредством графика. Обычно графики чертятся с помощью самопишущих приборов. Данный способ задания функции используется при физических, медицинских измерениях.

 

Классификация функций по их свойствам

I. Основные простейшие функции:

1) постоянная 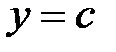, где .

2) степенная , где .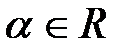

3) показательная .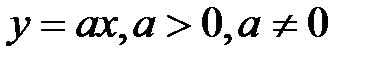

4) логарифмическая .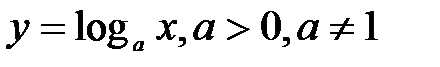

5) тригонометрическая , .                                                           

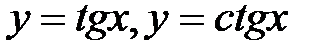6) обратные тригонометрические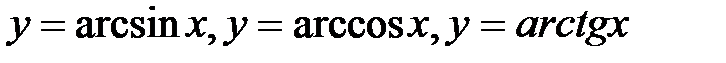

.

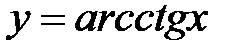I. Элементарные функции

Определение №1. Всякая функция, которая может быть явным образом задана с помощью формулы, содержащей лишь конечное число арифметических операций и конечное число суперпозиций основных простейших функций, называется элементарной функцией.

Элементарные функции обычно делятся на классы:

1) Многочлены (полиномы).

К ним относятся функции, которые могут быть заданы формулами вида: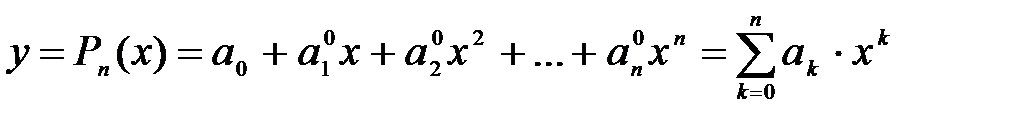

Если , то число  называется степенью данного многочлена.     

Многочлены называются целой рациональной функцией.

Определение №2. Многочлены первой степени называются линейными функциями .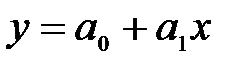

2) Дробно-рациональные функции.

К этому классу функций относятся функции, которые могут быть заданы в виде: 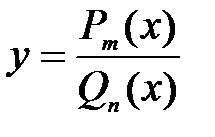, где  и 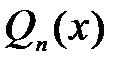 - многочлены степеней  и

.

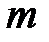
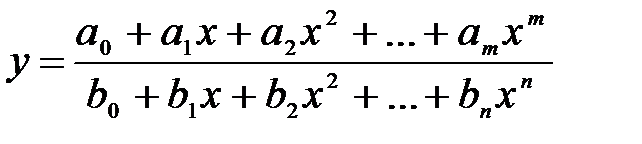Определение №3. Функция, представляющая собой отношение двух целых рациональных функций называется дробно-рациональной функцией.

Определение №4. Совокупность целых рациональных и дробно-рациональ­ных функций образует класс рациональных функций.

3) Иррациональные функции.

Определение №5. Иррациональной функцией называется функция, которая может быть задана с помощью суперпозиций конечного числа рациональных функций, степенных функций с рациональными показателями и четырех арифметических операций.

Пример: .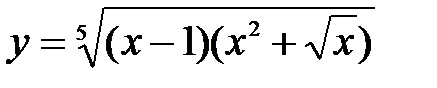

4) Трансцендентные функции.

Определение №6. Всякая функция не являющаяся рациональной и иррацио­нальной называется трансцендентной функцией.

Пример: ;  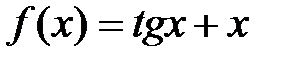и т.д.