Периодические функции

Определение №1. Функция , заданная на некотором множестве, называется периодической с периодом , где 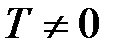, если  из этого множества, числа 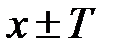 тоже входят в область задания функции и при этом справедливо равенство: .

Примеры:

Определение №2. Периодом функции называется наименьший из всех положительных периодов.

Пример: Функция 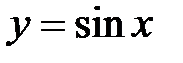 называется 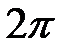-периодической, хотя ее периодом будут такие числа 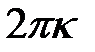, где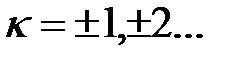

Чтобы построить график -периодической функции достаточно пост-роить его в пределах одного периода, т.е. от любого значения  до . Затем сдвигая построенный график вправо и влево на расстоянии 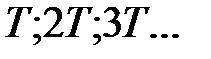, получим графическое представление функции на всем желаемом промежутке.

Модуль

Тема №3

Функции и их свойства. Операции над функциями. Композиция функций. Обратная функция. Предел функции

Лекция №10

1. Предел функции по Гейне и Коши.

2. Примеры.

3. Геометрический смысл предела функции в точке.

4. Эквивалентность двух определений.

5. Односторонние пределы.

6. Теорема о связи односторонних пределов функции в точке с пределом функции в точке.