2020-10-10
988
1. Кроме рассмотренного предела функции в точке существует такое понятие как предел в точке слева или предел в точке справа.
Определение №3. Число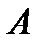 
называется правым пределом (или пределом справа) функции 
в точке 
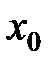, если для любой, сходящейся к 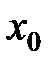последовательности значений аргумента 
, все элементы которой больше 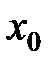, соответствующая последовательность значений функции 
сходится к 
.
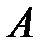Символически: 
или 
или 
.
Определение №4. Число 
называется левым пределом (пределом слева) функции 
в точке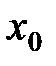 
, если для любой, сходящейся к 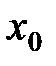, последо- вательности значений аргумента 
, все элементы которой меньше 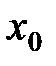, соответствующая последовательность значений функции 
сходится к .
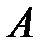Символически: 
или 
или 
.
Иными словами: Если бы в определении предела функции в точке потребовалось бы, чтобы х стремился к 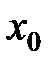не любым способом, а только слева, оставаясь все время меньше 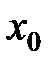, то получили бы определение предела функции в точке 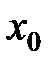слева.
Аналогично, если существует предел функции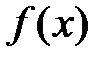 
в точке 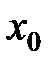при условии, что х стремился к 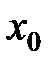только справа, оставаясь все время больше 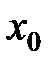, то такой предел называется пределом справа [2].
Определение №5. Пределы слева и справа функции в точке называются односторонними в отличие от предела функции в точке, который называется двусторонним.
Теперь рассмотрим равносильные определения односторонних пределов функции в точке слева и справа «на языке 
».
Определение №6. Число 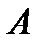называется правым пределом функции 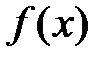в точке 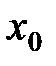, если 
существует такое 
, что для всех х, удовлетворяющих неравенствам 
, выполняется неравенство 
[2].
Символически:
Графически:
Рис.3.
Определение №7 («на языке 
»). Число называется левым пределом (пределом слева) функции 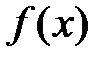в точке 
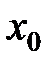, если
.
Символически: 
.
Графически:
Рис.4.
Пример 5. Функция 
(сигнум) имеет в точке 
левый и правый пределы функции в точке (рис. 5).
а) 
б) 
Рис.5.
Замечание №3. Не пишут 
, а пишут 
.
, а пишут 
[2].
Теорема о связи односторонних пределов функции в точке
