С пределом функции в точке

Теорема №2. Функция 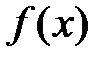 имеет в точке  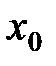предел тогда и только тогда, когда в этой точке существуют как правый, так и левый пределы функции и они равны. В этом случае предел функции в точке равен односторонним пределам.

Доказательство необходимости

1. Пусть 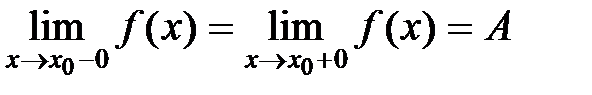. Нужно доказать, что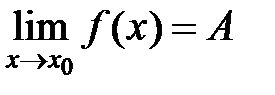

2. Согласно определениям предела функции в точке слева и справа, для  существуют такие числа 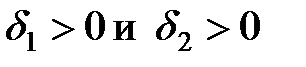, что для всех х, удовлет- воряющих неравенствам 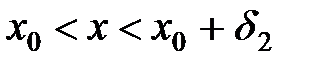  выполняется нера- венство .  

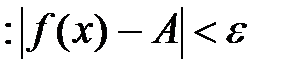3. Возьмем 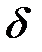 наименьшим из 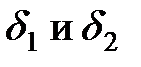, т.е. .

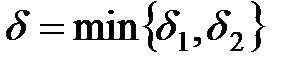4. Тогда для всех х, удовлетворяющих неравенству  будет выполняться неравенство .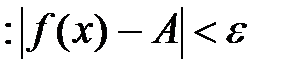

5. В соответствии с определением предела функции в точке по Коши последнее неравенство равносильно записи 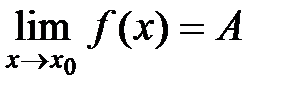.                   Ч.т.д.

Доказательство достаточности

1. Пусть теперь 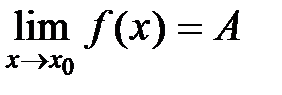. Нужно доказать, что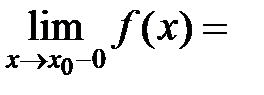

= .

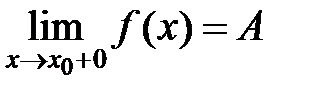2. Так как 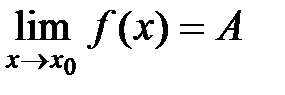, то согласно определению предела функции в точ ке, 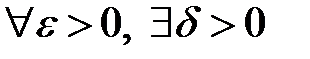, что для всех х, удовлетворяющих неравенству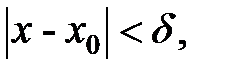 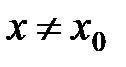 будет выполняться неравенство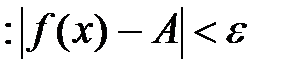

  3. Неравенство 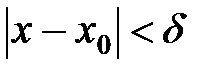 равносильно  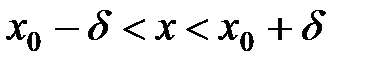или его можно записать так: .

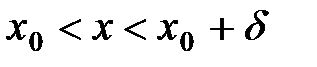4. Т.е. для последних двух неравенств справедливо .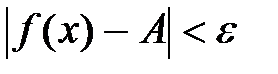

5. Следовательно, справедливы такие равенства согласно определениям односторонних пределов функции в точке слева и справа: 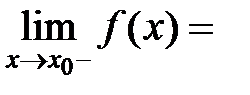 = 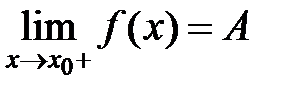[5].                                                                                       Ч.т.д.                                                                                      

Замечание №4. Если односторонние пределы различны: 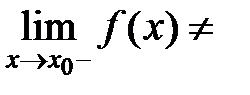 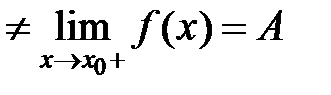или хотя бы один из пределов не существует, то не сущест- вует и предел функции в точке  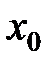[5].