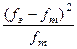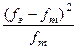Пример 1
Хекгаузена тематической апперцепции тест (НТАТ) – проективная методика исследования личности, направлен на оценку мотивационного аспекта личности. Выделяются категории мотивации достижения успеха и мотивации избегания неудачи. Х. Хекгаузен оперирует терминами «надежда на успех» и «боязнь неудачи».
По данной методике обследовано 113 [13, 284] студентов в возрасте от 20 до 35 лет. В данном исследовании разным испытуемым стимульный набор методики Хекгаузена (6 картин) предъявлялся в разном порядке. Было установлено, что в рассказах по картинкам с условным названием «Преподаватель и ученик» и «Мастер измеряет деталь» словесные формулировки, отражающие «боязнь неудачи» встречаются чаще, чем в рассказах по другим картинам, в особенности по картине «Улыбающийся юноша».
Эмпирическое распределение словесных формулировок, отражающих мотивы «надежды на успех» и «боязнь неудачи» представлена в табл. 11.
Таблица 11
Эмпирическое распределение словесных формулировок, отражающих мотивы «надежды на успех» и «боязнь неудачи».
|
| Разряды-картины методики | Количество вербальных реакций, отражающих | Всего | |||
| «надежда на успех» | «боязнь неудачи» | |||||
| 1 | «Мастер измеряет деталь» | А | 106 | 138 | Б | 244 |
| 2 | «Преподаватель и ученик» | В | 102 | 180 | Г | 282 |
| 3 | «В цехе у машины» | А | 108 | 34 | Е | 142 |
| 4 | «У двери директора» | Ж | 50 | 87 | З | 137 |
| 5 | «Человек в бюро» | И | 99 | 57 | К | 156 |
| 6 | «Улыбающийся юноша» | Л | 115 | 20 | М | 135 |
| Всего | 580 | 516 | 1096 | |||
Вопрос 1:
Можно ли утверждать, что разные картины методики Хекгаузена обладают разной побудительной силой в отношении мотивов:
· «надежды на успех»;
· «боязнь неудачи».
Для ответа на данный вопрос необходимо принять решение о выборе метода математической обработки.
Так как данные уже получены и представлены в таблице, чтобы ответить на данный вопрос, необходимо принять решение о задаче, условии решения задачи и выборе критерия.
Задача: Выявить различия в распределении признака:
· «надежда на успех»;
· «боязнь неудачи».
Условие решения задачи: Сопоставить эмпирическое распределение реакции признака «надежда на успех» и реакции признака «боязнь неудачи» с теоретическим (равномерным распределением).
Это позволит проверить, равномерно ли распределяются реакции «надежды на успех» по шести картинам и равномерно ли распределяются реакции «боязнь неудачи» по шести картинам.
Метод математической обработки: c2 – критерий Пирсона
Количество наблюдений достаточно велико, поэтому можно было бы использовать критерий Колмогорова-Смирнова. Однако в исследовании картины предъявлялись разным испытуемым в разной последовательности, то есть отсутствует однонаправленное изменение признака в какую-либо сторону: все разряды (картины) следуют друг за другом в случайном порядке.
Поэтому методом выбора математической обработки является критерий c2, а не критерий λ.
Расчет критерия c2 при сопоставлении распределения реакций «надежды на успех» по 6 картинам с равномерным распределением представлен в табл. 3.18.
Таблица 12
Расчет критерия c2 при сопоставлении распределения реакций «надежды на успех» по 6 картинам, с равномерным распределением.
| Разряды – картины методики | Частоты реакции «надежды на успех» | fэ – fт | (fэ – fт)2 |
| ||
| fэмп. | fтеор. | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 2 3 4 5 6 | «Мастер измеряет деталь» «Преподаватель и ученик» «В цехе у машины» «У двери директора» «Человек в бюро» «Улыбающийся юноша» | 106 102 108 50 99 115 | 96,67 96,67 96,67 96,67 96,67 96,67 | 9,33 5,33 11,33 -46,67 2,33 18,33 | 87,05 28,41 128,37 2178,09 5,43 335,99 | 0,90 0,29 1,33 22,53 0,06 3,48 |
| Суммы | 580 | 580 | 0 | 2763,34 | 28,59 | |
АЛГОРИТМ
расчета критерия c2
| Расчет критерияc2 | Пример |
| I. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (столбец 1,2). | I. Таблица №8 (столбец 1,2) |
II. Расчет теоретической частоты для равномерного распределения по формуле:
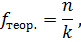 где n – количество наблюдений (сумма эмпирических частот психологического признака).
k – количество разрядов.
(столбец 3)
где n – количество наблюдений (сумма эмпирических частот психологического признака).
k – количество разрядов.
(столбец 3)
| II.
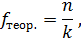 где n – количество наблюдений – это количество (сумма эмпирических частот) реакции «надежды на успех» у 113 испытуемых по 6 картинам.
Количество разрядов – это количество картин – 6.
где n – количество наблюдений – это количество (сумма эмпирических частот) реакции «надежды на успех» у 113 испытуемых по 6 картинам.
Количество разрядов – это количество картин – 6.
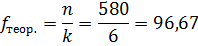 (столбец 3)
(столбец 3)
|
| III. Подсчитать разности между эмпирической и теоретической частотой по каждому разряду (строке) и записать их в столбец 4. | III. Столбец 4 (fэ – fт) |
| IV. Возвести в квадрат полученные разности и занести их в столбец 5. | IV. Столбец 5 (fэ – fт)2 |
| V. Разделить полученные квадраты разностей на теоретическую частоту и занести в столбец 6. | V. Столбец 6 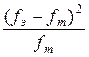
|
VI. Просуммировать значения столбца 6. Полученную сумму обозначить как 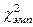
| VI. Сумма столбца 6 равна 28,59
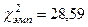
|
VII. Определить число степеней свободы по формуле
n = k – 1
где k – количество разрядов признака
Если n=1, внести поправку на «непереносимость». Это означает, что все расчеты производим по известному алгоритму, но с одним добавлением: перед возведением в квадрат разности частот необходимо уменьшить абсолютную величину этой разности на 0,5:
· (fэмп – fтеор – 0,5) – столбец 4
· (fэмп – fтеор – 0,5)2 – столбец 5
· 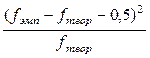 – столбец 6
Для данного числа степеней свободы n по таблице «Критические значения критерия c2 для уровней статистической значимости р ≤ 0,05 и р ≤ 0,01 при разном числе степеней свободы V» определяем критическое значение – столбец 6
Для данного числа степеней свободы n по таблице «Критические значения критерия c2 для уровней статистической значимости р ≤ 0,05 и р ≤ 0,01 при разном числе степеней свободы V» определяем критическое значение 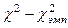 . .
| VII. Количество степеней свободы n определяем по формуле: n = k – 1
n = 6 – 1 = 5
Поправка на непереносимость не нужна.
По таблице определяем критические значения c2 для n = 5
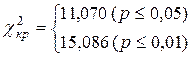
|
VIII. Если 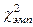 меньше критического значения меньше критического значения 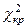 , то расхождения между распределениями статистически недостоверны.
Если , то расхождения между распределениями статистически недостоверны.
Если 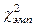 равно критическому значению равно критическому значению 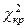 или превышает его, расхождения между распределениями статистически достоверны. или превышает его, расхождения между распределениями статистически достоверны.
| VIII.
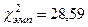
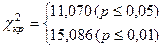
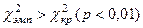
|
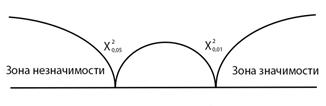 IX. Построить «ось значимости» IX. Построить «ось значимости»
| IX. Построим «ось значимости»

|
| X. Вывод. | X. Распределение реакции «надежды на успех» по шести картинам методики Хекгаузена достоверно отличается от равно-мерного распределения (р < 0,01). |
Пример 2
Расчет критерия c2 при сопоставлении распределения реакций «боязнь неудачи» по 6 картинам с равномерным распределением представлен в табл. 13.
Таблица 13
Расчет критерия c2 при сопоставлении распределения реакций «боязнь неудачи» по 6 картинам с равномерным распределением.
| Разряды – картины методики | Частоты реакции «боязнь неудачи» | fэ – fт | (fэ – fт)2 |
| ||
| fэмп. | fтеор. | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 2 3 4 5 6 | «Мастер измеряет деталь» «Преподаватель и ученик» «В цехе у машины» «У двери директора» «Человек в бюро» «Улыбающийся юноша» | 138 180 34 87 57 20 | 86 86 86 86 86 86 | 52 94 -52 1 -29 -66 | 2704 8836 2704 1 841 4356 | 31,44 102,74 31,44 0,01 9,78 50,65 |
| Суммы | 516 | 516 | 0 | 19442 | 226,06 | |
1. Определяем количество степеней свободы n по формуле:
n = k – 1
n = 6 – 1 = 5
Поправка на «непереносимость» не нужна. Производить расчет критерия c2 необходимо по общему алгоритму.
2. Рассчитываем теоретические частоты для равномерного распределения по формуле:
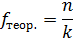
где n – количество наблюдений – это сумма эмпирических частот реакций «боязнь неудачи», n = 516.
k – количество разрядов – это число стимульных картин, k = 6.
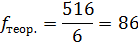
3. Подсчитываем разности между эмпирической и теоретической частотой по каждому разряду (строке) и записываем в столбец 4.
4. Возводим в квадрат полученные разности и заносим их в столбец 5.
5. Разделить полученные квадраты разностей на теоретическую частоту и занести в столбец 6.
6. Определяем 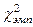 по сумме значений столбца 6.
по сумме значений столбца 6.
7. По таблице «Критические значения критерия c2» определяем критические значения c2 при n = 5.
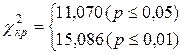
8.  Построим «ось значимости»
Построим «ось значимости»
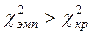
Вывод: распределение проявлений «боязнь неудачи» по шести стимульным картинам достоверно отличается от равномерного распределения (р < 0,01).
Пример 3
Результаты, полученные в эксперименте по заучуванню ряда из 20 чисел для 100 испытуемых предоставлены в таблице. С помощью критерия Пирсона (c2 – критерия) проверить гипотезу о нормальности распределения случайной величины Х – количества заученных чисел.
Таблица 14
 2020-10-10
2020-10-10 536
536