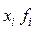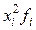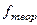Количество заученных чисел каждым из 100 испытуемых

4	7	10	4	7	10	4	7	10	7	10	7
7	10	7	13	10	7	10	13	10	7	7	10
10	10	10	13	10	13	10	7	7	10	13	10
16	13	10	7	13	10	16	16	7	10	16	19
7	13	10	19	10	10	10	10	16	10	10	7
7	7	10	7	10	13	10	13	13	10	13	13
13	7	7	10	13	13	10	10	7	16	10	16
10	10	13	10	10	10	10	10	7	10	10	7
13	10	10	16

 

Решение.

1. Превратим данные в статистический ряд (по возрастанию)

4	4	4	7	7	7	7	7	7	7
7	7	7	7	7	7	7	7	7	7
7	7	7	7	7	7	7	10	10	10
10	10	10	10	10	10	10	10	10	10
10	10	10	10	10	10	10	10	10	10
10	10	10	10	10	10	10	10	10	10
10	10	10	10	10	10	10	10	10	10
10	10	13	13	13	13	13	13	13	13
13	13	13	13	13	13	13	13	13	13
16	16	16	16	16	16	16	16	19	19

 

2. Построим статистическое распределение выборки.

 

Статистическим распределением выборки называют перечень вариант х_і (возможных значений случайной величины Х)и соответствующих им частот f_i.

Статистическое распределение выборки имеет вид:

 

xi	4	7	10	13	16	19
fi	3	24	45	18	8	2

 

Сумма всех частот равняется объему выборки n:

 

n =3+24+45+18+8+2=100.

 

3. Построим полигон частот.

 

Полигоном частот называется ломаная, отрезки которой соединяют точки с координатами (x₁, f₁),...,(x_m, f _m).

xi

fi

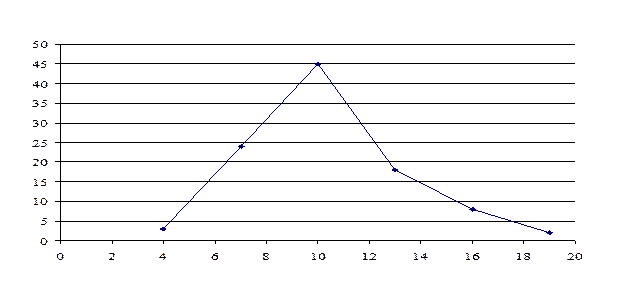
По виду полигона частот выдвигаем гипотезу о нормальном законе распределения.

 

Найдем выборочную среднюю, дисперсию, среднее квадратическое отклонение. Для этого составим расчетную таблицу:

Таблица 15

xi	fi
4	3	12	48
7	24	168	1176
10	45	450	4500
13	18	234	3042
16	8	128	2048
19	2	38	722
Суммы	100	1030	11536

 

Среднее арифметическое вычисляем по формуле:

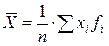,                                                 (1)

где n – объем выборки,

х_i – значения случайной величины,

f_i – частоты значений случайной величины.

Имеем, 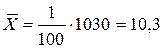, где 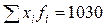 – число из последней строки расчетной таблицы.

Дисперсию обозначим через D и вычисляем по формуле

                                           (2)

Из таблицы 11, получим:

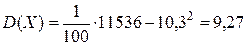
Стандартное отклонение определяем, используя формулу

.                                           (3)

Для нашей задачи имеем:

5. Найдем выравнивающие частоты, предполагая, что распределение является нормальным.

Выравнивающие (теоретические) частоты рассчитывают по формуле:

                                               (4)

где n – количество наблюдений (объем выборки);

h – шаг, т.е. расстояние между соседними значениями Х (в распределении с равноотстающими значениями х_i: ;

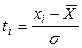 нормируемые отклонения;

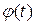– табличные значения функции  (см. приложение – таблицу 6).

Вычисления будем производить в таблице 16 по алгоритму (см. ниже)

 

Таблица 16

Расчет теоретических значений частот (выравнивающих частот) в предположении нормальности распределения случайной величины

1	2	3	4	5
i	xi	ti
1	4	-2,06	0,0478	4,7
2	7	-1,08	0,2227	21,9
3	10	-0,10	0,397	38,9
4	13	0,88	0,2709	26,6
5	16	1,86	0,0707	6,9
6	19	2,84	0,0071	0,7
Σ				99,6

 

 

АЛГОРИТМ