2020-10-09
123
Определение 2.1. Производной функции в точке 
называется предел отношения приращения функции 
к приращению аргумента 
, когда приращение аргумента стремится к нулю (если этот предел существует), то есть
или 
.
Значение производной функция 
в точке обозначается 
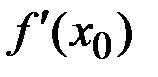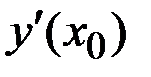или 
, или 
. Операция нахождения производной называется дифференцированием; функция , имеющая производную в каждой точке интервале 
, называется дифференцируемой в этом интервале.
Теорема 2.1.(О связи между непрерывностью и дифференцируемостью)
Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.
З а м е ч а н и е 2.1. Обратное утверждение неверно: непрерывная функция может не иметь производной.
Производная широко используется при изучении различных процессов. Рассмотрим задачу о скорости.
Пусть материальная точка движется неравномерно вдоль некоторой прямой. Закон движения (зависимость пройденного расстояния от времени) известен и имеет вид 
. Ставится задача нахождения мгновенной скорости точки. Моменту времени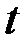 
соответствует значение расстояния 
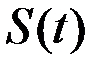. Моменту времени 
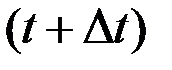соответствует значение расстояния 
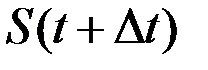. За промежуток времени 
точкой пройдено расстояние 
.
|
|
|
Средняя скорость 
движения точки определяется формулой 
и зависит от значения : чем меньше , тем точнее средняя скорость выражает скорость движения точки в данный момент времени. При очень малом значении (
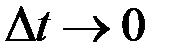) получается формула для нахождения мгновенной скорости точки 
.
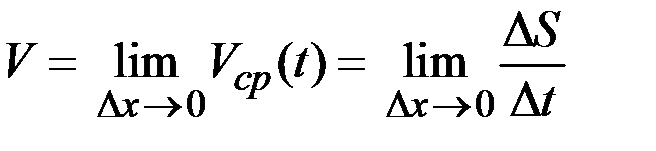В этом и заключается механический смысл производной: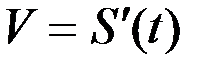 
– скорость прямолинейного движения материальной точки в момент времени 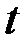есть производная от пути 
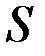по времени .
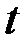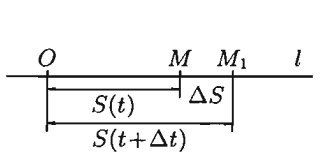
Рис 2.1
Рассмотрим задачу о касательной.
Рассматривается непрерывная кривая – график непрерывной функции . Через точк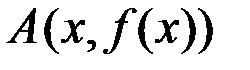и 
и 
(
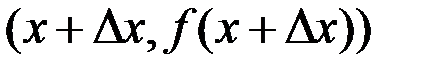этого графика проведена прямая 
– секущая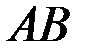 
(рис 7.2.) (она составляет угол 
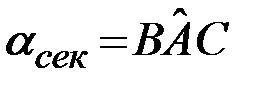с осью 
).
Угловой коэффициент секущей определяется по формуле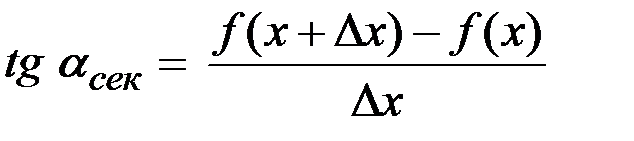 
или 
.
При уменьшении значения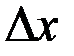 
, точка 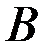приближается вдоль кривой к точке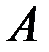 
. При очень малом значении (
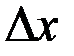) секущая
приближается к своему предельному положению и переходит в касательную 
– прямую 
(рис 7.2.), при этом 
(
– угол, который составляет касательная с осью ).
При очень малом значении 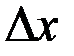() получается формула для нахождения углового коэффициента касательной к графику функции в точке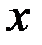 
.
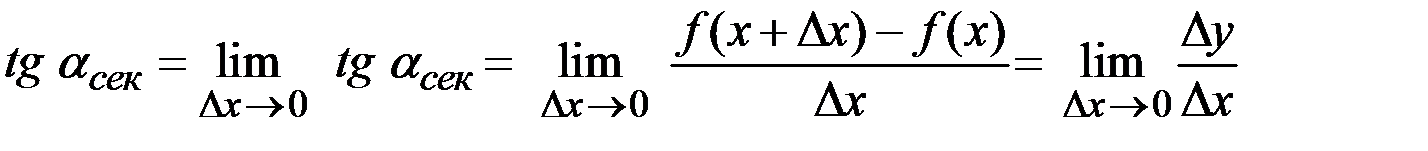В этом и заключается геометрический смысл производной: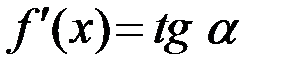 
– угловой коэффициента касательной к графику функции в точке 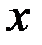есть производная этой функции в точке .
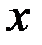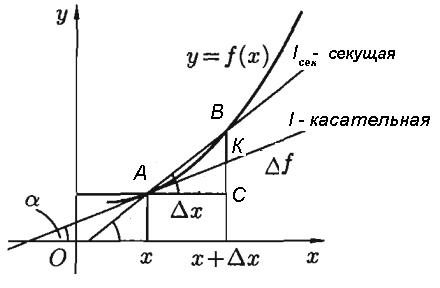
Рис. 2.2.
З а м е ч а н и е 2.2. Если точка касания имеет координаты 
, то, используя уравнение прямой, проходящей через данную точку в заданном направлении, можно записать уравнение касательной 
.
|
|
|
З а м е ч а н и е 2.3. Уравнение нормали к кривой принимает вид
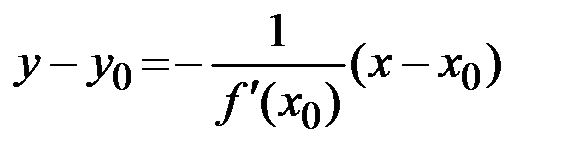, где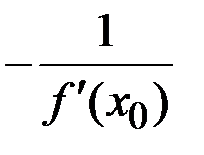 
– угловой коэффициента нормали (прямой, перпендикулярной касательной в точке касания ).
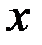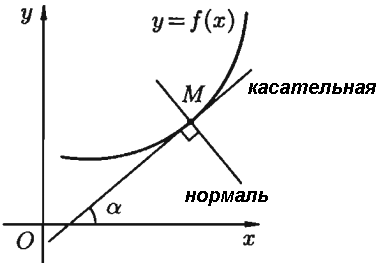
Рис. 2.3.
