Здесь приводятся теоремы, которые облегчают нахождение пределов функции. Формулировки теорем для случаев, когда 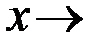
 и
и 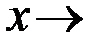
 . В приводимых теоремах будем считать, что
. В приводимых теоремах будем считать, что 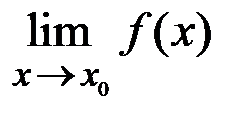 и
и 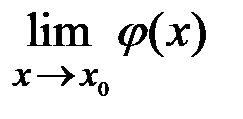 существуют.
существуют.
Теорема1.11. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
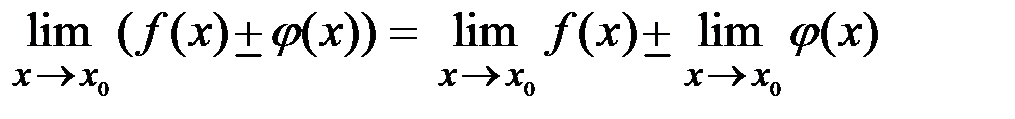 .
.
З а м е ч а н и е 1.2. Теорема справедлива для любого конечного количества функций.
Теорема 1.12. Функция может иметь только один предел при 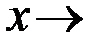
 .
.
Теорема 1.13. Предел произведения двух функций равен произведению их пределов:
 .
.
Теорема 1.14. Постоянный множитель можно выносить за знак предела 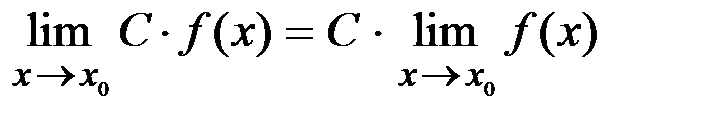 .
.
Теорема 1.15. Предел степени с натуральным показателем равен той же степени предела:
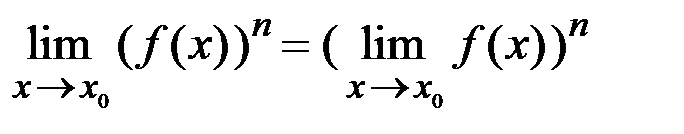 .
.
Теорема 1.16. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю:
 ,
,  .
.
З а м е ч а н и е 1.3. Во многих вопросах анализа достаточно только убедится в существовании предела функции, поскольку не всякая функция, даже ограниченная, имеет предел.
Далее приводятся признаки существования пределов.
Теорема 1.17. (О пределе промежуточной функции)
Если функция 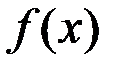 заключена между двумя функциями
заключена между двумя функциями 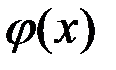 и
и 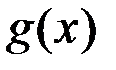 , стремящимися к одному и тому же пределу, то она также стремится к этому пределу, то есть если
, стремящимися к одному и тому же пределу, то она также стремится к этому пределу, то есть если
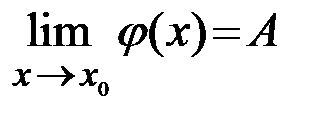 ,
, 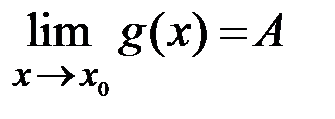 и
и 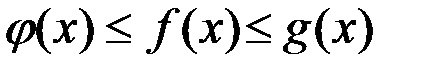 ,
,
то 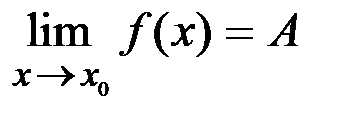 .
.
Теорема 1.18. (О пределе монотонной функции)
Если функция 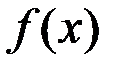 монотонна и ограниченапри
монотонна и ограниченапри  или при
или при 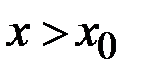 , то существует соответственно ее левый предел
, то существует соответственно ее левый предел 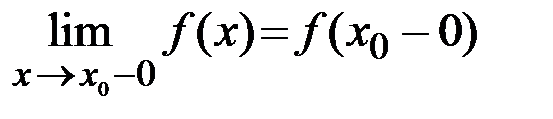 или ее правый предел
или ее правый предел 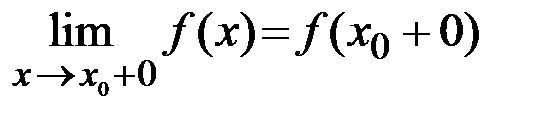 .
.
Следствие 1.3. Ограниченная монотонная последовательность  имеет предел.
имеет предел.
Замечательные пределы
Первый замечательный предел.
При вычислении пределов выражений, содержащих тригонометрические функции, часто возникает предел вида 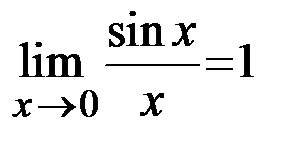 , называемый первым замечательным пределом. Использование данного предела позволяет раскрывать неопределенности вида
, называемый первым замечательным пределом. Использование данного предела позволяет раскрывать неопределенности вида 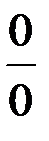 .
.
Приведем далее следствияиз первого замечательного предела.
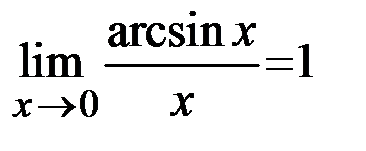 ,
, 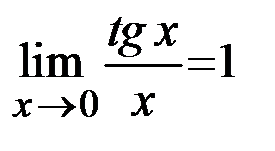 ,
, 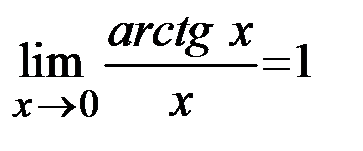 , а также
, а также
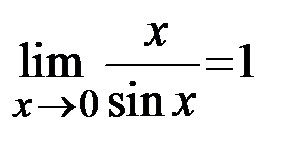 ,
, 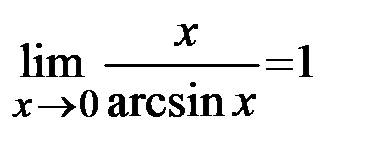 ,
, 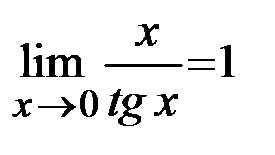 ,
,  .
.
 2020-10-09
2020-10-09 200
200








