Второй замечательный предел

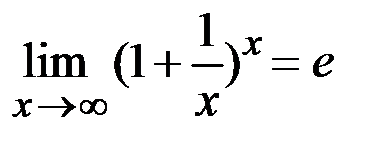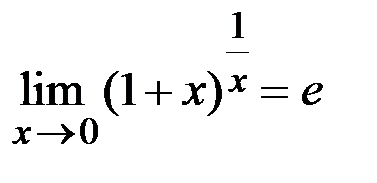Равенства    и  называют в торым замечательным пределом. Использование данного вида пределов позволяет раскрывать неопределенности вида .

Непрерывность функции. Точки разрыва, их классификация.

Пусть функция   определена в точке  и в некоторой окрестности этой точки.

Определение 1.6. Функция называется непрерывной в точке , если существует предел функции в этой точке и он равен значению функции в этой точке, то есть .

Определение 1.7. Функция называется непрерывной на интервале , если она непрерывна в каждой точке этого интервала.

Пусть функция  определена на интервале . Разность 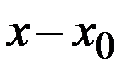 называется приращением аргумента и записывается , .

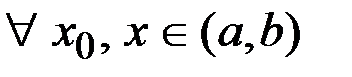Разность соответствующих значений функции называется приращением функции и записывается , или .

Можно ввести еще одно определение непрерывности функции в точке  в других обозначениях.

Определение 1.8. Функция называется непрерывной в точке , если бесконечно малому приращению аргумента соответствует бесконечно малое приращение, то есть функции в этой точке и он равен значению функции в этой точке, то есть .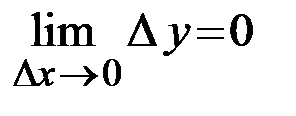

Далее рассматривается функция ,   определенная на некотором интервале .

Точки, в которых нарушается непрерывность функции, называются точками разрыва. Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

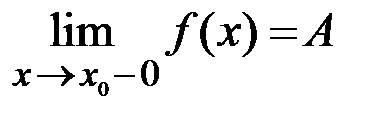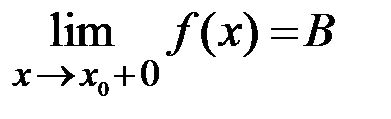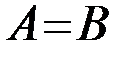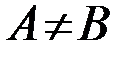Если в точке разрыва существуют конечные пределы функции слева  и справа , то  – то точка разрыва первого рода. При этом  если , то  – то точка устранимого   разрыва первого рода; если , то  – то точка конечного разрыва первого рода.

Точка    – точка разрыва второго рода функции , если хотя бы один односторонний предел не существует или равен бесконечности.