Прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой, называется асимптотой кривой.
Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Прямая  (см. Рис 1.2)является вертикальной асимптотой графика функции
(см. Рис 1.2)является вертикальной асимптотой графика функции  , если
, если 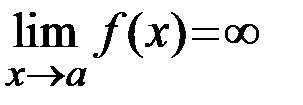 или
или  , или
, или  .
.
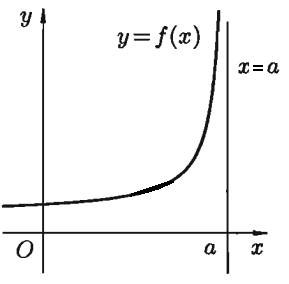
Рис. 1.2
Для нахождения вертикальных асимптот нужно найти те точки графика, вблизи которых функция неограниченно возрастает.
Уравнение наклонной асимптоты имеет вид 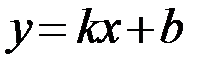 (см. Рис 6.3)с коэффициентами
(см. Рис 6.3)с коэффициентами  и
и 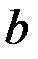 , которые определяются по формулам:
, которые определяются по формулам: 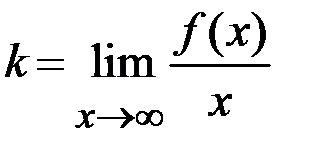 и
и  . Если хотя бы один из пределов
. Если хотя бы один из пределов 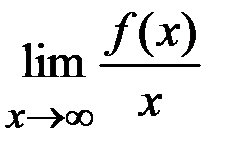 или
или 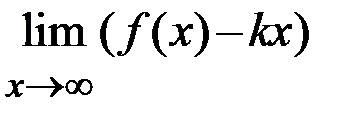 не существует или равен бесконечности, то кривая
не существует или равен бесконечности, то кривая  не имеет наклонной асимптоты.
не имеет наклонной асимптоты.

Рис. 1.3
Если 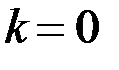 , а
, а  , то
, то  – уравнение горизонтальной асимптоты (см. Рис 1.4).
– уравнение горизонтальной асимптоты (см. Рис 1.4).

Рис. 1.4
График функции может иметь различные асимптоты при  и при
и при  , поэтому следует рассматривать отдельно случай
, поэтому следует рассматривать отдельно случай  и случай
и случай  .
.
ПРОИЗВОДНАЯ ФУНКЦИИ
Определение производной;
 2020-10-09
2020-10-09 271
271








