Прежде всего, укажем свойства, которые непосредственно вытекают из определения неопределенного интеграла.
1. 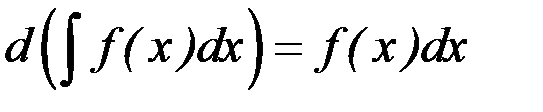 ,
, 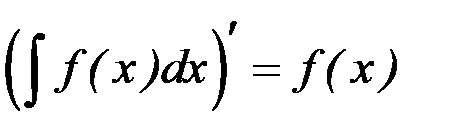 .
.
2. 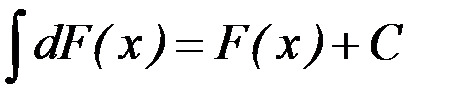 .
.
Следующие два свойства называются линейными свойствами неопределенного интеграла.
3. 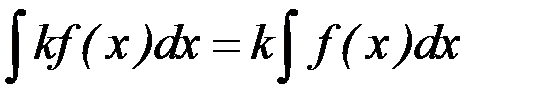 .
.
4. 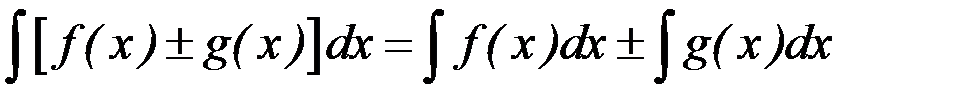 .
.
Отметим свойство инвариантности формулы интегрирования.
5. Если 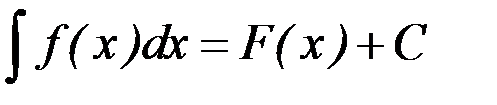 , то и
, то и 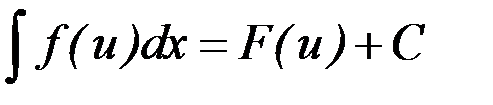 , где
, где  – произвольная функция, имеющая непрерывную производную.
– произвольная функция, имеющая непрерывную производную.
Таблица основных неопределенных интегралов
1. 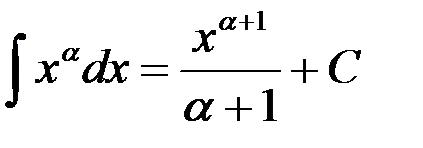 ,
, 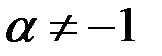 .
.
2. 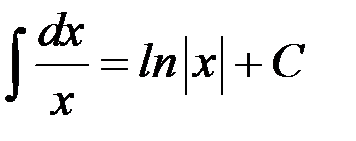 ,
, 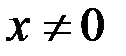 .
.
3. 
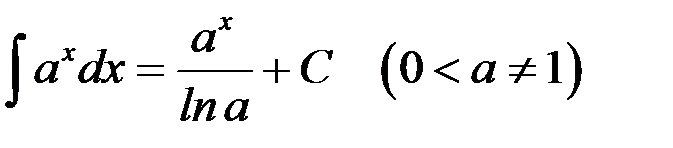 .
.
4. 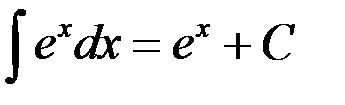 .
.
5.  .
.
6. 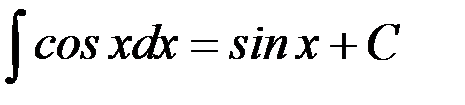 .
.
7.  .
.
8.  .
.
9.  .
.
10. 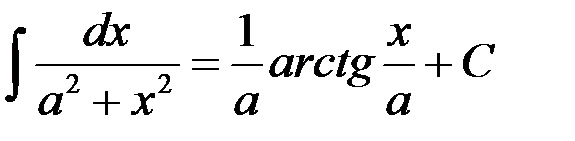 .
.
11.  .
.
12.  .
.
13. 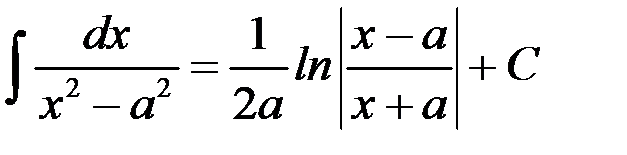 .
.
14. 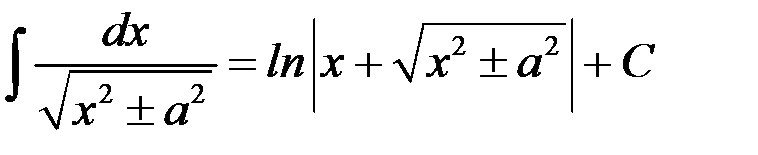 .
.
Основные методы интегрирования
Метод непосредственного интегрирования
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
Метод подстановки
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования. При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 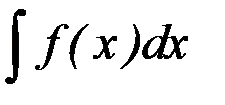 . Сделаем подстановку
. Сделаем подстановку 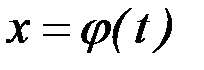 , где
, где  – функция, имеющая непрерывную производную. Тогда
– функция, имеющая непрерывную производную. Тогда  и на основании свойства инвариантности формулы интегрирования получаем формулу интегрирования подстановкой или формулой замены переменных
и на основании свойства инвариантности формулы интегрирования получаем формулу интегрирования подстановкой или формулой замены переменных
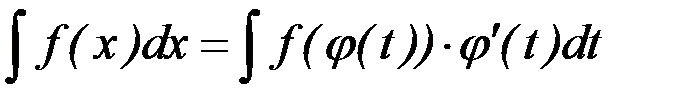 .
.
После нахождения интеграла правой части этого равенства следует перейти от новой переменной интегрирования  назад к переменной
назад к переменной 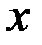 .
.
Иногда целесообразно подбирать подстановку в виде  , тогда
, тогда 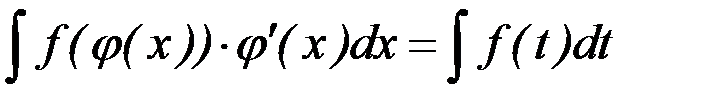 . Другими словами, формулу (10.1) можно применять справа налево.
. Другими словами, формулу (10.1) можно применять справа налево.
С помощью метода замены переменной можно вывести следующие основные правила интегрирования:
1. Если  , то
, то 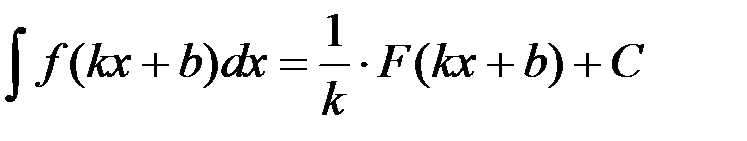 ;
;
2. 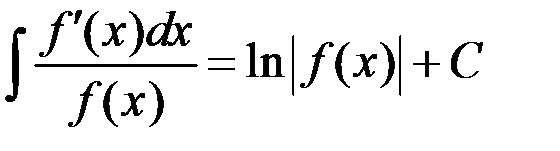 ;
;
3.  .
.
 2020-10-09
2020-10-09 177
177








