2020-10-09
265
Одна из основных задач дифференциального исчисления – нахождение производной заданной функции. Множество вопросов математического анализа и приложений в разнообразных науках приводит к другой задаче: по данной функции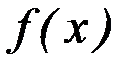 
найти такую функцию 
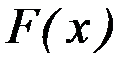, производная которой равна функции .
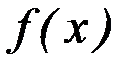Функция 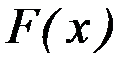называется первообразной функции 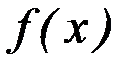на интервале 
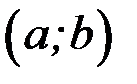, если для любого 
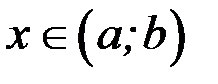выполняется равенство 
.
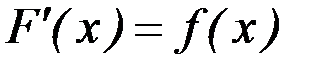Например, первообразной функции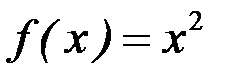 
, 
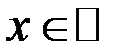, является функция 
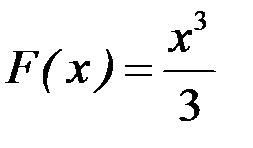, так как 
.
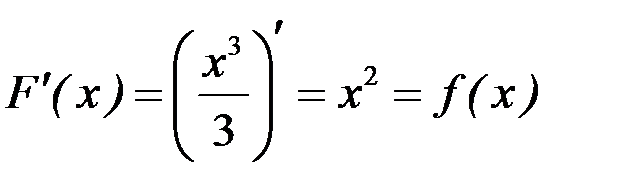Очевидно, что первообразными будут также любые функции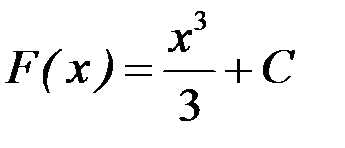 
, где 
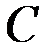– постоянная, поскольку
, .
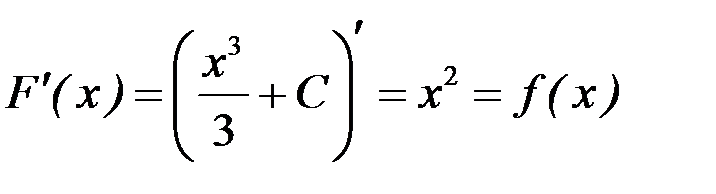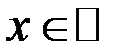Теорема 5.1. Если функция 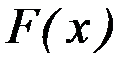является первообразной функции 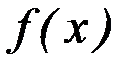на 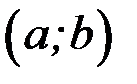, то множество всех первообразных для 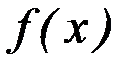задается формулой 
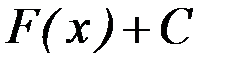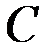, где – постоянное число.
Множество всех первообразных функций 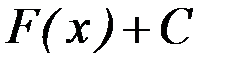для 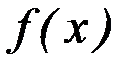называется неопределенным интегралом от функции 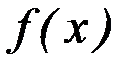и обозначается символом 
.
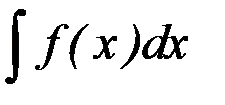Таким образом, по определению
.
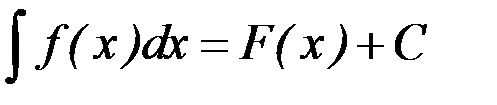Здесь 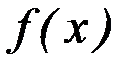называется подынтегральной функцией, 
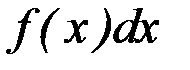– подынтегральным выражением, 
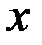– переменной интегрирования, 
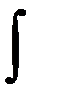– знаком неопределенного интеграла (это стилизованная латинская буква 
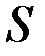, означающая суммирование).
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции. Интегрирование является операцией, обратной дифференцированию. Для проверки правильности выполнения интегрирования нужно продифференцировать результат и получить при этом подынтегральную функцию.
Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых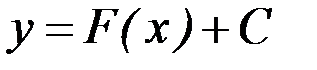 
, где каждому числовому значению 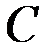соответствует определенная кривая семейства. График каждой первообразной (кривой) называется интегральной кривой.
