2020-10-11
162
Свойства вейвлет-функций,
· Локализация. Вейвлет-функции должны быть непрерывными, интегрируемыми, иметь компактный носитель и быть локализованными как во времени (в пространстве), так и по частоте. Если вейвлет-функция в пространстве сужается, то ее "средняя" частота повышается, спектр вейвлет-функции перемещается в область более высоких частот и расширяется. Этот процесс должен быть линейным – сужение функции вдвое должно повышать его "среднюю" частоту и ширину спектра также вдвое.
Вейвлет-функцию можно считать хорошо локализованной при выполнении условий:
ψ(t) ≤ C/(1+|t|)1+ε, ψ(f) ≤ C/(1+|f|)1+ ε, С=const, при ε> 0.
· Нулевое среднее значение, т.е. выполнение условия для нулевого момента:
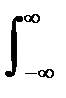ψ(t) dt = 0,
что обеспечивает выделение локальных особенностей сигналов в пределах вейвлетного носителя на уровне региональных изменений и тренда, нулевое усиление постоянной составляющей сигналов, нулевое значение частотного спектра вейвлет-функции при ψ=0, и локализацию ее спектра в виде полосового фильтра с центром на определенной (доминирующей) частоте ω0. Для анализа мелкомасштабных флюктуаций и особенностей высокого порядка, как правило, требуются и нулевые значения определенного количества последующих моментов:
|
|
|
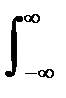tmψ(t) dt = 0. (3.1)
Такие вейвлет-функции называются вейвлетами m-го порядка.
· Ограниченность. Необходимое и достаточное условие:
||ψ(t)||2 = 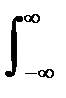|ψ(t)|2 dt < ¥ (3.2)
Оценка ограниченности и локализации может выполняться с использованием выражений:
|ψ(t)| < 1/(1+|t|n), или |Ψ(ω)| < 1/(1+|ωo|n), (3.3)
где ωo – средняя частота вейвлет-функции. Число n должно быть как можно больше.
Автомодельность базиса или самоподобие. Форма всех базисных вейвлет-функций ψab(t) должна быть подобна материнскому вейвлету ψ(t), т.е. должна оставаться одной и той же при сдвигах и масштабировании (растяжении/сжатии), иметь одно и то же число осцилляций.
В основе вейвлет-преобразований, в общем случае, лежит использование двух непрерывных, взаимозависимых и интегрируемых по независимой переменной функций:
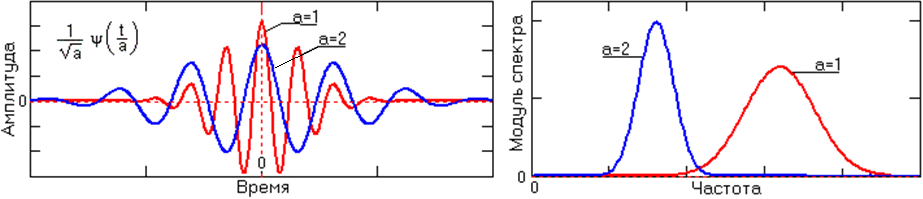
· Вейвлет-функции y(t), как psi-функции времени с нулевым значением интеграла и частотным фурье-образом Y(ω). Этой функцией, которую обычно и называют материнским вейвлетом, выделяются локальные особенности сигнала. В качестве вейвлетов обычно выбираются функции, хорошо локализованные и во временной, и в частотной области. Пример временного и частотного образа функции приведен на рис. 3.10.
Масштабирующей функции ψ(t), как временной скейлинг-функции phi с единичным значением интеграла, которой выполняется грубое приближение
· (аппроксимация) сигнала.
