Рис. 3.10. Вейвлетные функции в двух масштабах

Phi-функции присущи не всем, а, как правило, только ортогональным вейвлетам. Они необходимы для преобразования нецентрированных и достаточно протяженных сигналов при раздельном анализе низкочастотных и высокочастотных составляющих.

Непрерывное вейвлет-преобразование   (НВП, CWT- Continious Wavelet Transform).

Непрерывным вейвлет-преобразованием (или вейвлетным образом) функции s(t) Î L²(R) называют функцию двух переменных:

С(a,b) = ás(t), y(a,b,t)ñ = 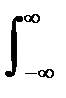s(t) y(а,b,t) dt, a, b Î R, a ≠ 0.                       (3.4)

где вейвлеты y(a,b,t) º y_ab(t) – масштабированные и сдвинутые копии порождающего вейвлета y(t) Î L²(R), совокупность которых создает базис пространства L²(R).  Для обработки изображений используется другой вид преобразования – дискретный.

Дискретное вейвлет-преобразование.  При обработке данных на ПК может выполняться дискретизированная версия непрерывного вейвлет-преобразования с заданием дискретных значений параметров (a, b) вейвлетов с произвольным шагом Δa и Δb. В результате получается избыточное количество коэффициентов, намного превосходящее число отсчетов исходного сигнала, которое не требуется для реконструкции сигналов.

Дискретное вейвлет-преобразование (ДВП) обеспечивает достаточно информации, как для анализа сигнала, так и для его синтеза, являясь вместе с тем экономным по числу операций и по требуемой памяти. ДВП оперирует с дискретными значениями параметров а и b, которые задаются, как правило, в виде степенных функций:

a = а_о^-m, b = k·а_о^-m, a_o > 1, m, k Î I,

где I – пространство целых чисел {-¥, ¥}, m – параметр масштаба, k – параметр сдвига. Базис пространства L²(R) в дискретном представлении:

ψ_mk(t) = |а_о|^m/2ψ(а_о^mt-k), m,k Î I, ψ(t) Î L²(R).                                        (3.5)

    Вейвлет-коэффициенты прямого преобразования:

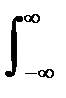C_mk= s(t)ψ_mk(t)dt.                                                                                      (3.6)

Значение 'a' может быть произвольным, но обычно принимается равным 2, при этом преобразование называется диадным вейвлет-преобразованием. Для диадного преобразования разработан быстрый алгоритм вычислений, аналогичный быстрому преобразованию Фурье, что предопределило его широкое использование при анализе массивов цифровых данных.

Обратное дискретное преобразование для непрерывных сигналов при нормированном ортогональном вейвлетном базисе пространства:

s(t) =  C_mkψ_mk(t).                                  (3.7)

Как и для непрерывного вейвлет-преобразования, обратное дискретное преобразование (3.7) не может выполнить восстановление нецентрированных сигналов в силу нулевого первого момента вейвлетных функций и, соответственно, центрирования значения вейвлет-коэффициентов C_mk при прямом вейвлет-преобразовании. Поэтому при обработке числовых массивов данных дискретные вейвлеты используются, как правило, в паре со связанными с ними дискретными скейлинг-функциями.[4,5]

Достоинства и недостатки вейвлетных преобразований.

· Вейвлетные преобразования обладают всеми достоинствами преобразований Фурье.

· Вейвлетные базисы могут быть хорошо локализованными как по частоте, так и по времени. При выделении в сигналах хорошо локализованных разномасштабных процессов можно рассматривать только те масштабные уровни разложения, которые представляют интерес.

· Вейвлетные базисы, в отличие от преобразования Фурье, имеют много разнообразных базовых функций, свойства которых ориентированы на решение различных задач. Базисные вейвлеты могут реализоваться функциями различной гладкости.

Недостатком вейвлетных преобразований является их относительная

· сложность.

Практическое использование вейвлет-преобразований связано, в основном, с дискретными вейвлет-функциями как в силу повсеместного использования цифровых методов обработки данных, так и в силу ряда различий дискретного и непрерывного вейвлет-преобразований.

Непрерывные вейвлет-функции дают несколько более наглядное представление результатов анализа в виде поверхностей вейвлет-коэффициентов по непрерывным переменным. На рис. 3.11 анализируемый сигнал состоит из двух модулированных гауссианов. Преобразование вейвлетом Морлета четко показывает пространственную и их частотную локализацию.[7]

Рис. 3.11 Пространственная и частотная локализация

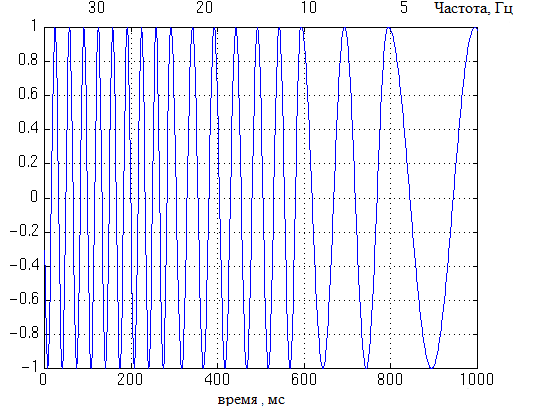Для наглядного отображения преимущества Вейвлет-преобразования относительно преобразования Фурье, рассмотрим тот же нестационарный сигнал: