Силовой расчет механизма начинаем с наиболее удаленной от ведущего звена группы Ассура ABCO2.
Группу ABCO2 вычерчиваем отдельно в масштабе схемы механизма и в том же положении.
Прикладываем силы веса 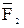 и
и 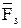 в центрах тяжести, и силы инерции:
в центрах тяжести, и силы инерции: 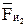 - против ускорения центра тяжести S2;
- против ускорения центра тяжести S2; 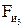 - против ускорения
- против ускорения 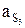 , но не в центре тяжести S3, а в центре качания звена (точка К), расположенном на расстоянии, мм:
, но не в центре тяжести S3, а в центре качания звена (точка К), расположенном на расстоянии, мм:
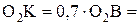 0,7 ∙ 76 = 53. (3.8)
0,7 ∙ 76 = 53. (3.8)
В этом случае 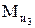 не определяем и заменяющую пару сил (
не определяем и заменяющую пару сил ( и
и  ) не прикладываем.
) не прикладываем.
Момент пары сил инерции  представим эквивалентной парой сил, Н:
представим эквивалентной парой сил, Н:
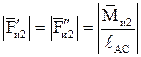 ,
, 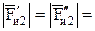
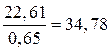 . (3.9)
. (3.9)
Освобождаем группу от связей и прикладываем вместо них реакции, которые представляем в виде двух составляющих: тангенциальной, направленной перпендикулярно к оси звена, и нормальной, направленной вдоль звена (направление произвольно).
Реакцию в шарнире А представим в виде двух составляющих – 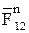 и
и  , а шарнира O2 – в виде
, а шарнира O2 – в виде 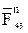 и
и  .
.
Составляем векторное уравнение равновесия сил, действующих на группу Ассура 2-3, начиная со 2-го звена и заканчивая третьим:
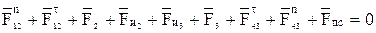 . (3.10)
. (3.10)
Силы 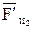 и
и 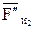 в уравнение не вписываем, так как это уравнение решается построением плана сил и они взаимно уравновешивают друг друга.
в уравнение не вписываем, так как это уравнение решается построением плана сил и они взаимно уравновешивают друг друга.
Из уравнения моментов относительно точки В для звена 2 определяем составляющую 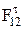 , Н:
, Н:
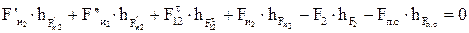 , (3.11)
, (3.11)
откуда
 ; (3.12)
; (3.12)
(размеры плеч 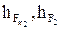 ,
, 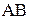 и т.д. снимаем с чертежа в миллиметрах).
и т.д. снимаем с чертежа в миллиметрах).
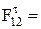
 .
.
Так как знак составляющей 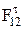 изменился на противоположный, ее действительное направление также меняется в противоположную сторону.
изменился на противоположный, ее действительное направление также меняется в противоположную сторону.
Из уравнения моментов относительно точки B для звена 3 определяем составляющую  , Н:
, Н:
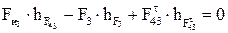 , (3.13)
, (3.13)
откуда
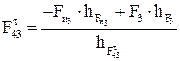 ; (3.14)
; (3.14)
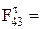
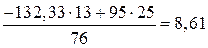 .
.
Сила 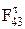 меняет своё направление на противоположное.
меняет своё направление на противоположное.
Выписываем значения всех сил, Н, действующих на группу Ассура 2 - 3:
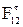 = 303,71; F2 = 162,5;
= 303,71; F2 = 162,5; 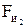 = 343,95;
= 343,95; 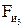 = 132,33;
= 132,33;
Fпс =1250; F3 = 95; 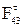 = 8,61.
= 8,61.
Задаемся произвольным масштабом плана сил, Н / мм:
 7.
7.
Вычисляем длины векторов, изображающих эти силы, мм:
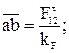

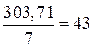 ;
; 
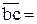
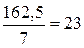 ;
;

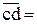
 ;
; 
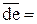
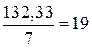 ; (3.15)
; (3.15)
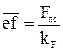 ;
; 
 ;
; 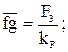
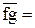
 ;
;
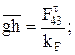
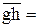
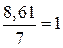 .
.
Отрезок 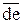 изобразим на плане в виде точки.
изобразим на плане в виде точки.
Строим план сил.
От произвольной точки а – начала плана сил – параллельно силе 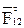 откладываем вектор
откладываем вектор 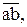 изображающий эту силу; от конца вектора
изображающий эту силу; от конца вектора  параллельно силе
параллельно силе 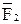 откладываем в том же направлении вектор
откладываем в том же направлении вектор 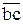 и далее векторы всех сил. Через точку a параллельно звену AB проводим линию действия
и далее векторы всех сил. Через точку a параллельно звену AB проводим линию действия  , а через точку h параллельно звену BC – линию действия силы
, а через точку h параллельно звену BC – линию действия силы 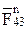 . Точка пересечения i этих линий определяет векторы
. Точка пересечения i этих линий определяет векторы 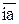 – силы
– силы 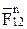 и
и 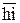 – силы
– силы 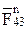 . Умножив длины этих векторов на масштаб плана сил kF, получим их значения, Н:
. Умножив длины этих векторов на масштаб плана сил kF, получим их значения, Н:
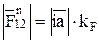 ;
; 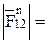 203 ∙ 7 = 1421; (3.16)
203 ∙ 7 = 1421; (3.16)
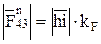 ;
;  157 ∙ 7 = 1099. (3.17)
157 ∙ 7 = 1099. (3.17)
Векторы 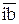 и
и 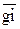 , являясь геометрическими суммами векторов
, являясь геометрическими суммами векторов  и
и 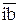 ,
, 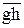 и
и 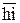 соответственно, представляют в масштабе полные реакции
соответственно, представляют в масштабе полные реакции 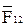 и
и 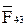 , Н:
, Н:
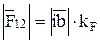 ;
; 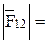 207 ∙ 7 = 1449; (3.18)
207 ∙ 7 = 1449; (3.18)
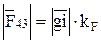 ;
; 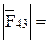 157 ∙ 7 = 1099. (3.19)
157 ∙ 7 = 1099. (3.19)
Для определения реакции в шарнире B составим уравнение равновесия сил, действующих на звено 2:
 (3.20)
(3.20)
Векторы сил 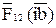 ,
, 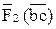 и
и 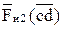 уже есть на плане сил; соединив точки i и d, получаем реакцию
уже есть на плане сил; соединив точки i и d, получаем реакцию 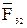 , действующую со стороны звена 3 на звено 2, Н:
, действующую со стороны звена 3 на звено 2, Н:
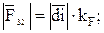 (3.21)
(3.21)
 233 ∙ 7 = 1631.
233 ∙ 7 = 1631.
Реакция со стороны звена 2 на звено 3 равна по значению и противоположна по направлению  :
:
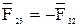 . (3.22)
. (3.22)
Производим расчет ведущего звена.
На ведущее звено действуют вес  , сила инерции
, сила инерции  , со стороны звена 2 – реакция
, со стороны звена 2 – реакция 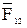 , со стороны стойки – реакция
, со стороны стойки – реакция 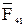 . Кроме этих сил, в точку А кривошипа перпендикулярно к оси звена приложим уравновешивающую силу
. Кроме этих сил, в точку А кривошипа перпендикулярно к оси звена приложим уравновешивающую силу  . Силы
. Силы 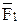 ,
, 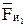 и
и  известны по значению и направлению, а силы
известны по значению и направлению, а силы 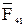 и
и 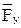 не известны.
не известны.
Для определения значения 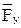 составляем уравнение моментов всех сил, действующих на звено 1, относительно точки О1, Н:
составляем уравнение моментов всех сил, действующих на звено 1, относительно точки О1, Н:
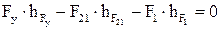 , (3.23)
, (3.23)
откуда
 (3.24)
(3.24)

 .
.
Определяем реакцию 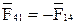 по значению и направлению путем построения плана сил согласно векторному уравнению:
по значению и направлению путем построения плана сил согласно векторному уравнению:
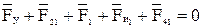 . (3.25)
. (3.25)
Выписываем значения всех сил, Н:
F1 = 50; F21 = 1449;  45,29; Fу = 1180,45.
45,29; Fу = 1180,45.
Произвольно задаемся масштабом:
 8 Н/мм.
8 Н/мм.
Вычисляем длины векторов всех сил для плана, мм:
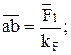
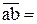
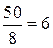 ;
;  ;
; 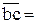
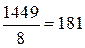 ;
;
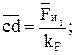
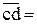
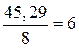 ;
; 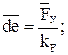
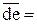
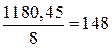 . (3.26)
. (3.26)
Соединив точки e и a, получаем реакцию в шарнире О1 (со стороны опоры 4 на звено 1), Н:
 (3.27)
(3.27)
 107 ∙ 8 = 856.
107 ∙ 8 = 856.
4 ПРОЕКТИРОВАНИЕ ЗУБЧАТОЙ ПРЯМОЗУБОЙ ПЕРЕДАЧИ С ЭВОЛЬВЕНТНЫМ ПРОФИЛЕМ ЗУБА
 2020-10-11
2020-10-11 348
348








