Векторные диаграммы гармонических токов и напряжений

Гармоническое колебание тока i(t) показано на   рис. 6.1. Оно характеризуется следую­щими основными параметрами: амп­литудой I_т; угловой частотой 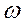, начальной фазой 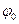. Функция i(t) носит название мгновенное значениетока.Амплитудой 1_т   называют максимальное абсолютное значение тока i(t).

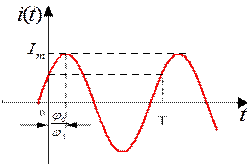
  Рис. 6.1

Аналитически гармоническое колебание можно за­писать в виде:

       i(t) = 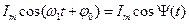                                                         (6.1)

где 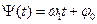 — текущая фаза(или просто фаза) гармонического колебания. Угловая частота  =

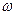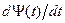
Гармо­ническое колебание можно выразить и в синусоидальной форме:

       i(t) = 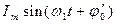  ,                                                                    (6.2)

                                          где .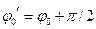

Наименьший промежуток времени, через который значения гармонической функции i(t) повторяются, называется периодом Т. Перио­д Т и угловая частота 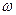  связаны соотношением

                             T = 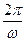.                                                                         (6.3)

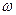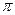Величина, обратная периоду, называется циклической часто­той: f = 1/Т. Угловая и циклическая частоты связаны между собою:   = 2 f.

Единицей измерения циклической частоты f является герц (Гц), угловой частоты 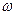— ради­ан в секунду (рад/с). Так как радиан — величина безразмерная, то ω измеряется в 1/с или .

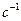Важными параметрами гармонических колебаний являются их действующее и среднее значения. Действующее значениегармо­нического тока

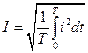                                                                                       (6.4)

Здесь i = i(t) — мгновенное значение гармонического тока.

Подставив значение i из (6.1) в (6.4), после интегрирования получим

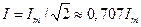                                              .                       (6.5)

Аналогично определяются мгновенное и действую­щее значения напряжения и ЭДС:

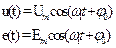
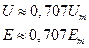
Действующие значения токов и напряжений (ЭДС) называют еще их среднеквадратическими значениями.

Среднее значениегармонического тока

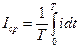                                            .                                                      (6.6)

Подставив значение i(t) из (3.1) в (3.6), получим, что 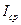= 0, соответственно  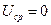и .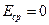

Рассмотрим гармонические колебания в резистивных, индуктивных и емкостных элементах.