Функции нескольких переменных

Определение: Переменная 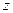 называется функцией двух переменных  и 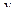, если каждой паре чисел  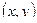из некоторого множества по определенному правилу или закону ставится в соответствие одно или несколько значений переменной .

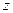Тот факт, что переменная 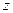 является функцией переменных  и 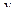, обычно записывают в виде 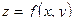. При этом переменные  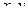называются независимыми переменными или аргументом, а переменная  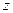– зависимой переменной, или функцией.

Множество пар чисел 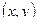, для которых определена функция 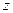, называется областью определения этой функции. Множество значений функции  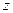называется областью изменения этой функции. Закон соответствия  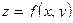может быть задан аналитически, таблично, графически, словесным образом и т.д. Математический анализ изучает преимущественно аналитически заданные функции.

Определение: Областью определения аналитически заданной функции 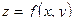 называется совокупность всех пар чисел 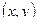, которым соответствует действительные значения функции.

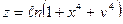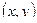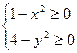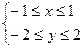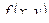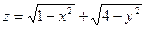Так, например, для функций , ,  область определения – множество всевозможных пар чисел . Для функции  область определения состоит из всех пар чисел, для которых   т.е.  область определения функции  будет изображаться некоторым множеством точек  плоскости. Функция  определена в прямоугольнике со сторонами ; .

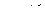Функция двух переменных 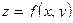 может быть геометрически изображена в виде поверхности. Графиком функции  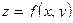в пространстве  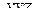является поверхность, представляющая собой геометрическое место , когда точка 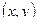 пробегает область определения функции. Для функции  изображающая её поверхность – параболоид вращения. Функция 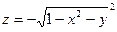 изображается нижней полусферой с центром  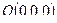радиуса .

Другим способом геометрической иллюстрации функции двух переменных является способ называемый линией уровня функции .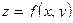

Определение: Линией уровня функции двух переменных 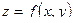 называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно 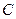. Число  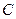в этом случае называется уровнем.