2020-10-12
189
РГЗ состоит из четырех задач. Задание на каждую задачу включает в себя ее формулировку и двадцать вариантов исходных данных.
Задача 1. Вычислить работу силы 
при перемещении точки приложения силы вдоль заданной кривой L от точки B до точки C, если значения параметра t в точках B и C заданы.
| Номер варианта | Сила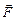 
| Параметрические уравнения кривой L | Значения параметра t в точках B и C |
| 1 |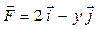 
| 
| 
|
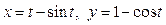
| 2 | 
| 
| 
|
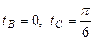
| 3 |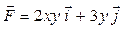 
| 
| 
|
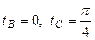
| 4 | 
| 
| 
|
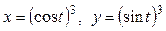
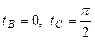
| 5 |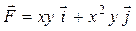 
| 
| 
|
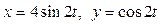
| 6 | 
| 
|
|
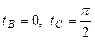
| 7 | 
| 
| 
|
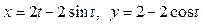
| 8 |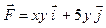 
| 
|
|
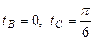
| 9 | 
| 
|
|
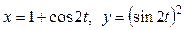
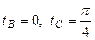
| 10 |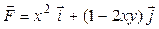 
| 
| 
|
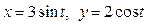
| 11 |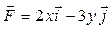 
| 
|
|
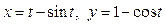
| 12 |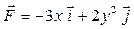 
|
| 
|
| 13 |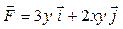 
| 
|
|
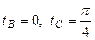
| 14 |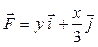 
| 
|
|
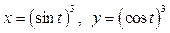
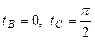
| 15 | 
| 
| 
|
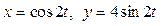
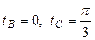
| 16 |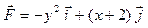 
| 
|
|
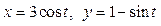
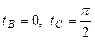
| 17 |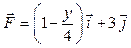 
| 
|
|
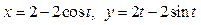
| 18 |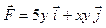 
| 
|
|
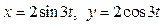
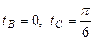
| 19 |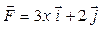 
| 
|
|
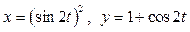
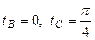
| 20 |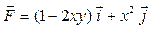 
| 
|
|
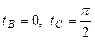
Задача 2. Задан радиус-вектор движущейся точки: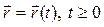 
. Найти векторы скорости и ускорения движения этой точки через 4 секунды после начала движения.
| № варианта | Радиус-вектор | № варианта | Радиус-вектор |
| 1 | 
| 2 | 
|
| 3 |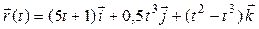 
| 4 | 
|
| 5 |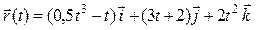 
| 6 |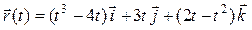 
|
| 7 |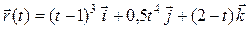 
| 8 | 
|
| 9 |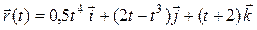 
| 10 |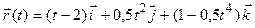 
|
| 11 |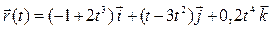 
| 12 |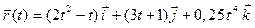 
|
| 13 |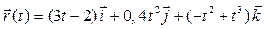 
| 14 |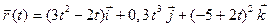 
|
| 15 |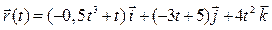 
| 16 |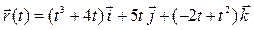 
|
| 17 |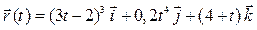 
| 18 |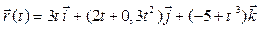 
|
| 19 | 
| 20 | 
|
Задача 3. Дано векторное поле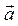 
и уравнение плоскости d.
| Номер варианта | Векторное поле 
| Уравнение плоскости d |
| 1 |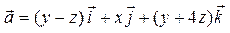 
| 2 x + 2 y + z – 2 = 0 |
| 2 |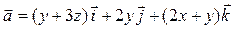 
| 2 x + 3 y + z – 1 = 0 |
| 3 |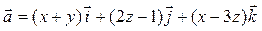 
| 3 x + 2 y + z – 6 = 0 |
| 4 |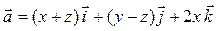 
| x + 2 y + 2 z – 2 = 0 |
| 5 |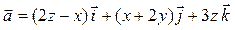 
| 3 x + y + 2 z – 3 = 0 |
| 6 |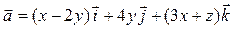 
| 4 x + y + 2 z – 2 = 0 |
| 7 |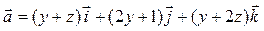 
| x + y + 2 z – 2 = 0 |
| 8 |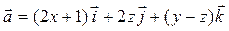 
| 2 x + 3 y + 4 z – 6 = 0 |
| 9 |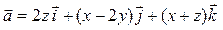 
| x + 2 y + 4 z – 4 = 0 |
| 10 |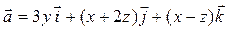 
| x + 5 y + z – 5 = 0 |
| 11 |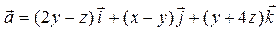 
| x - 2 y + z – 2 = 0 |
| 12 |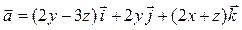 
| 2 x – 3 y + z – 3 = 0 |
| 13 |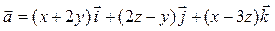 
| 2 x - 2 y + z – 6 = 0 |
| 14 |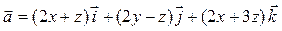 
| - x - 2 y + 2 z – 2 = 0 |
| 15 | 
| 3 x + y + 2 z – 3 = 0 |
| 16 |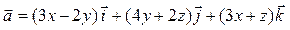 
| 3 x - y + 2 z – 2 = 0 |
| 17 |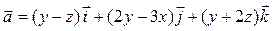 
| 2x +3 y + 2 z – 6 = 0 |
| 18 | 
| 2 x - 2 y + 4 z – 4 = 0 |
| 19 |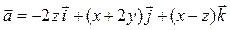 
| -x + 2 y + 2 z – 4 = 0 |
| 20 |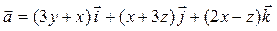 
| x + 5 y + z – 5 = 0 |
Требуется:
1) найти поток поля 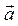через плоскость треугольника АВС и через плоскость AOB, где А, В, и С – точки пересечения плоскости d с координатными осями, в направлении нормали плоскости, ориентированной «от начала координат»; построить чертеж пирамиды ОАВС, где О – начало координат;
2) используя формулу Остроградского-Гаусса, вычислить поток поля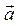 
через полную поверхность пирамиды ОАВС в направлении внешней нормали;
3) найти циркуляцию поля 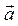по контуру треугольника АВС непосредственно и по формуле Стокса
Задача 4. Проверить, является ли векторное поле заданной силы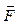 
потенциальным или соленоидальным. В случае потенциальности поля найти его потенциал и вычислить с помощью потенциала работу силы 
при перемещении единичной массы из точки M в точку N, где точки M и N заданы.
| Номер варианта | Сила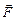 
| Точки M и N |
| 1 | 
| M (–1, 0, 0), N (1, 2, 1) |
| 2 | 
| M (0, –2, 1), N (1, 0, 0) |
| 3 | 
| M (1, –2, 0), N (3, 0, –1) |
| 4 | 
| M (0, –1, –2), N (1, –3, 0) |
| 5 |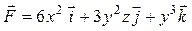 
| M (–2, 0, 1), N (–1, 1, 0) |
| 6 | 
| M (2, 1, 0), N (0, –1, 3) |
| 7 | 
| M (–1, 2, 1), N (0, 1, –1) |
| 8 |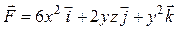 
| M (0, 1, –2), N (1, –2, –1) |
| 9 |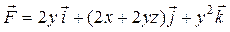 
| M (0, –1, 4), N (1, 0, 3) |
| 10 |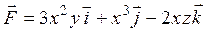 
| M (2, –2, 1), N (3, 0, –1) |
| 11 | 
| M (–1, 0, 0), N (1, -2, 1) |
| 12 |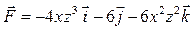 
| M (0, –2, 1), N (1, 0, 0) |
| 13 |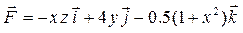 
| M (1, –2, 0), N (3, 0, –1) |
| 14 |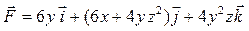 
| M (0, 1, 2), N (-1, 3, 0) |
| 15 |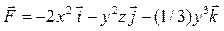 
| M (–2, 0, 1), N (–1, 1, 0) |
| 16 |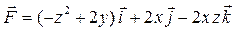 
| M (2, 0, 0), N (0, –1, 3) |
| 17 |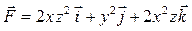 
| M (–1, 2, 1), N (0, 1, –1) |
| 18 | 
| M (1, –2, –1), N (0, 1, –2) |
| 19 | 
| M (1, 0, 3), N (0, –1, 4) |
| 20 |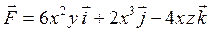 
| M (2, 2, 1), N (3, 0, –1) |
