Задача 1. Вычислить работу силы 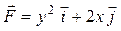 при перемещении точки приложения силы вдоль заданной кривой L:
при перемещении точки приложения силы вдоль заданной кривой L: 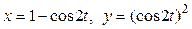 от точки B до точки C, если значения параметра t в точках B и C заданы:
от точки B до точки C, если значения параметра t в точках B и C заданы: 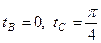 .
.
Решение.
Для вычисления работы используем криволинейный интеграл II рода (формула (3)): 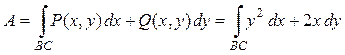 .
.
Составленный криволинейный интеграл сводим к определенному интегралу, используя параметрические уравнения кривой ВС:
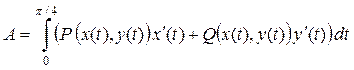 .
.
Для заданной кривой получаем:
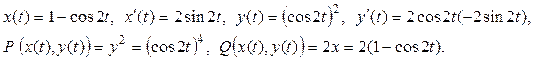
Таким образом, для нахождения работы нужно вычислить определенный интеграл:
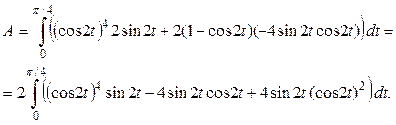
Сделаем замену переменной в определенном интеграле:
 ,
, 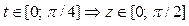 ,
,
тогда получим: 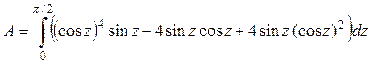 .
.
Используем прием «подведение под знак дифференциала части подинтегральной функции»: 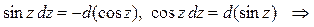
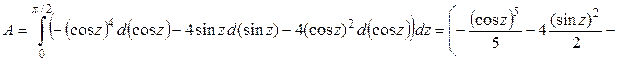

Ответ: 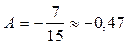 ед. работы.
ед. работы.
Задача 2. Задан радиус-вектор движущейся точки:
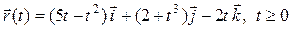 . Найти векторы скорости и ускорения движения этой точки через 2 минуты после начала движения.
. Найти векторы скорости и ускорения движения этой точки через 2 минуты после начала движения.
Решение.
Вектор-функция задана в координатной форме: 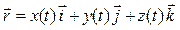 .
.
Найдем первые и вторые производные ее проекций x (t), y (t) z (t) по аргументу t:
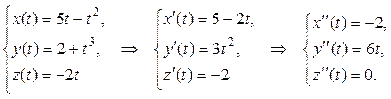
Найдем векторы скорости и ускорения движения точки по формулам (4) и (5):
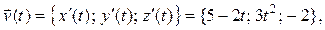
 .
.
Через 2 минуты после начала движения векторы скорости и ускорения будут:
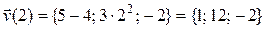 ,
, 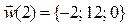 .
.
Ответы: 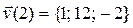 ,
, 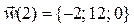 .
.
Задача 3. Дано векторное поле 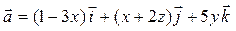 и уравнение плоскости d: 3 x + y + 2 z – 3 = 0. Требуется:
и уравнение плоскости d: 3 x + y + 2 z – 3 = 0. Требуется:
1) найти поток поля  через плоскость треугольника АВС где А, В, и С – точки пересечения плоскости d с координатными осями, в направлении нормали плоскости, ориентированной «от начала координат»; построить чертеж пирамиды ОАВС, где О – начало координат;
через плоскость треугольника АВС где А, В, и С – точки пересечения плоскости d с координатными осями, в направлении нормали плоскости, ориентированной «от начала координат»; построить чертеж пирамиды ОАВС, где О – начало координат;
2) используя формулу Остроградского-Гаусса, вычислить поток поля 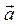 через полную поверхность пирамиды ОАВС в направлении внешней нормали.
через полную поверхность пирамиды ОАВС в направлении внешней нормали.
Решение.
1) Чтобы вычислить поток поля  через плоскость треугольника АВС используем формулу (6): ПАВС =
через плоскость треугольника АВС используем формулу (6): ПАВС = 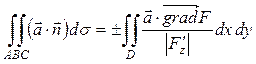 , где D – проекция треугольника АВС на плоскость xOy, F – функция, задающая плоскость d, которой принадлежит треугольник АВС.
, где D – проекция треугольника АВС на плоскость xOy, F – функция, задающая плоскость d, которой принадлежит треугольник АВС.
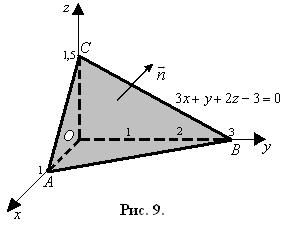 Для построения чертежа найдем точки А, В, и С пересечения плоскости d с координатными осями:
Для построения чертежа найдем точки А, В, и С пересечения плоскости d с координатными осями:
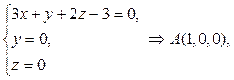
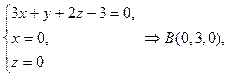
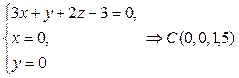 .
.
Построим чертеж пирамиды, отложив на координатных осях точки А, В, С и соединив их с началом координат O (рис. 9).
Из уравнения плоскости d: 3 x + y + 2 z – 3 = 0, которое имеет вид F (x, y, z) = 0, находим  .
.
Поскольку все три проекции градиента положительные, то этот вектор образует с координатными осями острые углы, т.е. направлен «от начала координат» по отношению к плоскости d. Это означает, что вектор 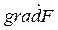 и орт «внешней» нормали
и орт «внешней» нормали 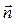 , указанный в задаче, совпадают по направлению, поэтому вычисление потока через плоскость треугольника АВС сводится к вычислению двойного интеграла: ПАВС = +
, указанный в задаче, совпадают по направлению, поэтому вычисление потока через плоскость треугольника АВС сводится к вычислению двойного интеграла: ПАВС = +  (перед интегралом ставим знак «+»), где AOВ – проекция треугольника ABC на плоскость xOy.
(перед интегралом ставим знак «+»), где AOВ – проекция треугольника ABC на плоскость xOy.
Для расстановки пределов интегрирования по треугольнику AOВ (рис. 10) найдем уравнение прямой АВ на плоскости xOy:
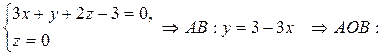
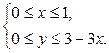
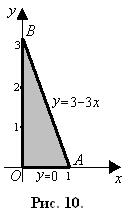 Вычислим
Вычислим 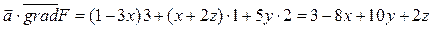 и получим подинтегральную функцию, подставив
и получим подинтегральную функцию, подставив  = 2 и
= 2 и 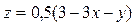 (из уравнения плоскости):
(из уравнения плоскости):
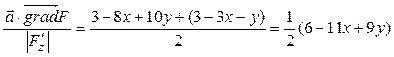 .
.
Таким образом, поток поля  через плоскость треугольника АВС:
через плоскость треугольника АВС:
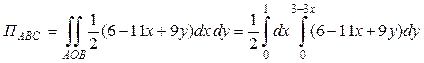 .
.
Вычислим внутренний интеграл по переменной y:
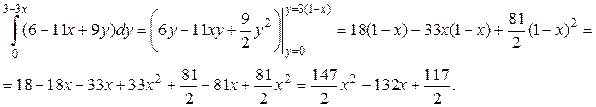
Вычислим внешний интеграл по переменной х:
 .
.
2) Чтобы вычислить поток поля  через полную поверхность пирамиды ОАВС, воспользуемся формулой Остроградского-Гаусса:
через полную поверхность пирамиды ОАВС, воспользуемся формулой Остроградского-Гаусса:
 .
.
Найдем дивергенцию этого поля по формуле (8): 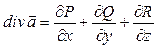 . Для поля
. Для поля  получаем:
получаем:
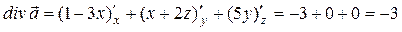 .
.
Вычислим поток поля  через полную поверхность пирамиды ОАВС:
через полную поверхность пирамиды ОАВС:
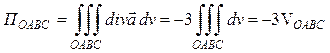 , где
, где 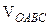 – объем пирамиды ОАВС. Этот объем можно вычислить, следующим образом:
– объем пирамиды ОАВС. Этот объем можно вычислить, следующим образом:
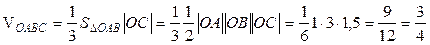 .
.
В результате получаем: 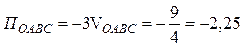 .
.
Ответы: ПABC = 8,5, рисунок 9; 2) ПОАВС = –2,25.
Задача 4. Проверить, является ли векторное поле силы 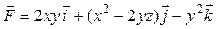 потенциальным или соленоидальным. В случае потенциальности поля найти его потенциал и вычислить с помощью потенциала работу силы
потенциальным или соленоидальным. В случае потенциальности поля найти его потенциал и вычислить с помощью потенциала работу силы 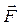 при перемещении единичной массы из точки M (0,1,0) в точку N (–1,2,3).
при перемещении единичной массы из точки M (0,1,0) в точку N (–1,2,3).
Решение.
Для проверки потенциальности векторного поля 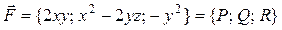 найдем его ротор по формуле (10):
найдем его ротор по формуле (10):
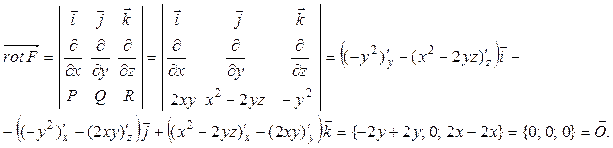
Следовательно, поле потенциально.
Для проверки соленоидальности поля найдем его дивергенцию по формуле (8):
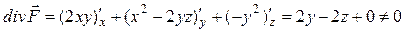 .
.
Следовательно, поле не соленоидально.
Для нахождения потенциала U (x,y, z) векторного поля возьмем фиксированную точку В (0,0,0), текущую точку С (x, y, z) и вычислим криволинейный интеграл  по ломаной ВEKC, звенья которой параллельны осям координат и E (x,0,0), K (x,y,0) (см. рис. 7). По формуле (12) получим:
по ломаной ВEKC, звенья которой параллельны осям координат и E (x,0,0), K (x,y,0) (см. рис. 7). По формуле (12) получим:
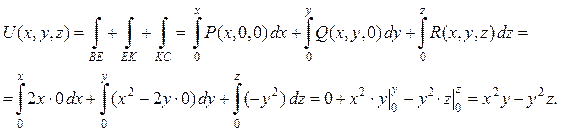
Получили потенциал поля 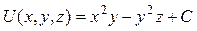 , где С – произвольная постоянная. Для проверки решения найдем градиент потенциала
, где С – произвольная постоянная. Для проверки решения найдем градиент потенциала 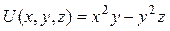 :
: 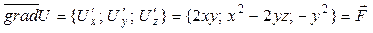 . Следовательно, потенциал поля силы найден верно.
. Следовательно, потенциал поля силы найден верно.
Найдем работу векторного поля 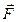 при перемещении единичной массы из точки M (0,1,0) в точку N (–1,2,3) по формуле (11):
при перемещении единичной массы из точки M (0,1,0) в точку N (–1,2,3) по формуле (11):
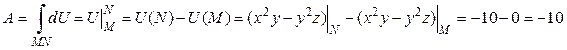 .
.
Ответы: поле 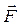 потенциально, не соленоидально;
потенциально, не соленоидально; 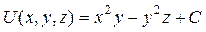 , где С – произвольная постоянная; работа А = –10.
, где С – произвольная постоянная; работа А = –10.
 2020-10-12
2020-10-12 320
320








