Потенциальное векторное поле и его потенциал

Векторное поле 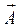 называется потенциальным, если существует такая функция 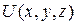, что 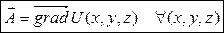. Функция U называется потенциалом векторного поля.

Из определения следует, что потенциальное векторное поле – это поле градиентов некоторого скалярного поля .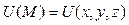

Признак потенциальности векторного поля: векторное поле 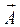 является потенциальным тогда и только тогда, когда его ротор – нулевой вектор:

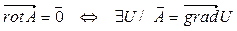.                       (11)

Одно из свойств потенциальных полей заключается в том, что если. 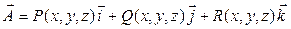 – потенциальное векторное поле, то его линейный интеграл по любой кривой MN, т.е. интеграл вида

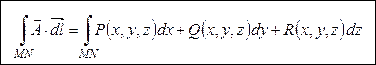
не зависит от формы кривой MN  и равен разности потенциалов в конечной и начальной точках:

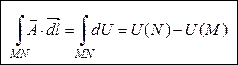.                       (12)

Это свойство можно использовать для нахождения потенциала векторного поля  при помощи криволинейного интеграла II рода. Для этого нужно взять фиксированную точку М (x ₀, y ₀, z ₀) и произвольную (текущую) точку N (x, y, z) и вычислить линейный интеграл по пути MN:

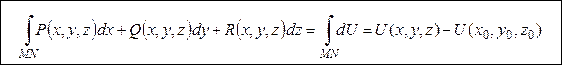. (13)

При этом получаем потенциал векторного поля 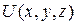 с точностью до произвольной постоянной.

После нахождения потенциала векторного поля его линейный интеграл 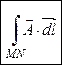 для любых заданных точек M и N можно вычислить по формуле (12).

Соленоидальное векторное поле.

Векторное поле 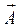 называется соленоидальным, если существует такое векторное поле 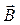, для которого поле  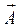является полем роторов: .

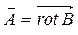Поле 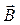 называется векторным потенциалом векторного поля .

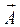Признак соленоидальности векторного поля: векторное поле 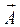 является соленоидальным тогда и только тогда, когда его дивергенция равна нулю:  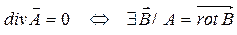 .                       (14)