Условие независимости криволинейного интеграла II рода от формы пути интегрирования

Для того чтобы криволинейный интеграл II рода 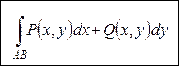не зависел от формы кривой AB, необходимо и достаточно, чтобы выполнялось условие: 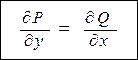(2)

во всех точках некоторой области D, содержащей кривую AB.

В этом случае существует функция U (x, y), такая, что подынтегральное выражение является ее полным дифференциалом:

Эту функцию можно восстановить (с точностью до константы) по ее полному дифференциалу, вычислив криволинейный интеграл по произвольному пути, соединяющему некоторую фиксированную точку (x ₀, y ₀) с «текущей» точкой (x, y):

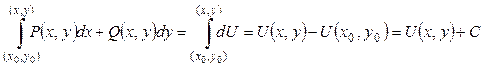. (3)

Векторная функция скалярного аргумента

Если каждому значению параметра t из некоторого промежутка 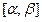ставится в соответствие по некоторому правилу f определенный вектор, то говорят, что задана вектор-функция скалярного аргумента t:

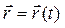. (4)

Откладывая вектор 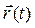при 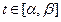от начала координат, получаем траекторию движения конца вектора, называемую годографом.

Проекции вектора 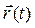на оси координат являются функциями аргумента t, поэтому можно записать:

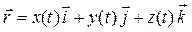Производная от вектора 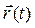по аргументу t определяется по формуле:

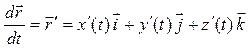а вторая производная соответственно:

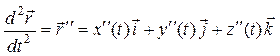Если параметр t – это время, то векторное уравнение (4) называют уравнением движения. Тогда вектор-производная называется скоростью движения:

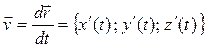, (5)

Скорость движения – это вектор, направленный по касательной к траектории движения (годографу) в соответствующей точке в сторону возрастания параметра t.

Вектор

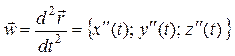. (6)