2020-10-12
368
Дивергенция (или расходимость) векторного поля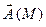 
в точке М – это предел отношения потока вектора 
через замкнутую поверхность σ, окружающую точку М, в направлении ее «внешней» нормали к объему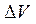 
, ограниченному этой поверхностью, при условии, что вся поверхность σ стягивается в точку М:
.
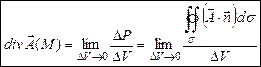Дивергенция – это дифференциальная(т.е. точечная) характеристика векторного поля; она является скалярной величиной и характеризует наличие источников (если 
) или стоков (если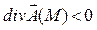 
) векторного поля в точке М.
Дивергенция векторного поля 
вычисляется по формуле:
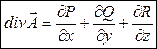. (8)
Формула Остроградского-Гаусса.
Формула Остроградского-Гаусса устанавливает связь между интегралом по замкнутой поверхности σ в направлении ее «внешней» нормали и тройным интегралом по области V, ограниченной этой поверхностью:
.
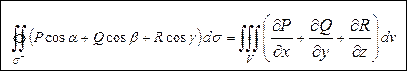Если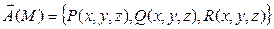 
– векторное поле, то векторная запись формулы Остроградского-Гаусса:
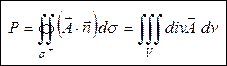, (9)
т.е. поток вектора через замкнутую поверхность σ в направлении ее «внешней» нормали равен тройному интегралу от дивергенции этого поля по области V, ограниченной этой поверхностью.
|
|
|
Потенциальные и соленоидальные векторные поля
Ротор векторного поля.
Ротором (вихрем) векторного поля 
называется вектор 
.
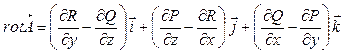Ротор – это векторная величина, которая является дифференциальной характеристикой векторного поля. Всякое векторное поле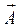 
сопровождает другое векторное поле 
его роторов.
Для вычисления ротора удобно использовать его запись в форме определителя:
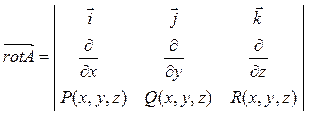(10)
где вектор 
– это векторно-дифференциальный оператор, называемый оператором Гамильтона «набла». При вычислении определителя умножению координат соответствует операция дифференцирования: 
.
