1) Смешанное произведение не меняется при циклических перестановках векторов:
(a×b) c =(b×c) a =(c ×a) b.
2) Смешанное произведение меняет знак на противоположный при перемене мест любых двух сомножителей:
(a×b) c=-(a´c)b=-(b´a)c=-(c´b)a
Доказательство. Все произведения по абсолютной величине дают объем одного и того же параллелепипеда, а знак произведений определяется ориентацией тройки сомножителей. При циклической перестановке векторов в тройке ориентация не меняется, при перестановке местами двух векторов в тройке ориентация меняется на противоположную ч.т.д.
Доказанное свойство позволяет записывать смешанное произведение в виде abc.
3) Три вектора a, b и c компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Необходимость следует из теоремы. Достаточность – тоже из теоремы, т.к. смешанное произведение некомпланарных векторов равно отличному от нуля объему параллелепипеда.
4) Смешанное произведение трех векторов, два из которых совпадают, равно нулю.
Т.к. такие векторы компланарны.
Выражение смешанного произведения через координаты векторов.
а =ах i +ay j +az k, b = bх i +by j +bz k, c = cх i +cy j +cz k
abc =(a×b) c= 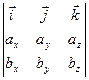 (cx i +cy j +cz k)=
(cx i +cy j +cz k)=
=(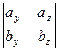 i-
i- 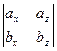 j+
j+ 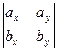 k) (cx i +cy j +cz k) =
k) (cx i +cy j +cz k) = 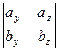 cx-
cx- 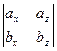 cy +
cy + 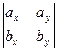 cz
cz
abc= 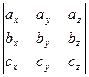
Т.о. объем параллелепипеда: V=± 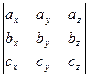
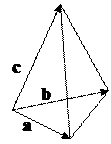 Vпир.=
Vпир.= 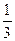 Sосн. пир. Н=
Sосн. пир. Н= 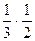 Sосн. парал.Н= ±
Sосн. парал.Н= ± 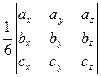
Следствие. Критерий компланарности: три вектора a,b и c компланарны тогда и только тогда, когда abc = 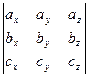 = 0 (в частности, любые два из них коллениарны).
= 0 (в частности, любые два из них коллениарны).
 2020-10-12
2020-10-12 199
199








