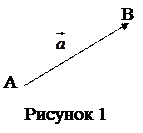 Вектором (свободным) называют совокупность всех одинаково направленных отрезков, имеющих одинаковую длину. Пусть
Вектором (свободным) называют совокупность всех одинаково направленных отрезков, имеющих одинаковую длину. Пусть  – направленный отрезок с началом в точке А и концом в точке В (рисунок 1). Этот отрезок
– направленный отрезок с началом в точке А и концом в точке В (рисунок 1). Этот отрезок  однозначно определяет некоторый вектор
однозначно определяет некоторый вектор  . В дальнейшем вектор
. В дальнейшем вектор  и направленный отрезок
и направленный отрезок  будут отождествляться, а использоваться будет тот из них, который в данном случае удобнее. Итак
будут отождествляться, а использоваться будет тот из них, который в данном случае удобнее. Итак 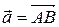 . Длина вектора
. Длина вектора  есть длина соответствующего отрезка
есть длина соответствующего отрезка  и обозначается
и обозначается 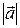 .
.
1.1.1 Определение. Векторы  и
и 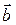 называются коллинеарными, если соответствующие им направленные отрезки параллельны. Векторы
называются коллинеарными, если соответствующие им направленные отрезки параллельны. Векторы  ,
, 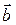 ,
, 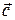 называются компланарными, если соответствующие им направленные отрезки параллельны одной плоскости.
называются компланарными, если соответствующие им направленные отрезки параллельны одной плоскости.
Два вектора  и
и 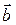 равны, если они коллинеарны, одинаково направлены и равны по длине. Пишут
равны, если они коллинеарны, одинаково направлены и равны по длине. Пишут  =
= 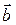 .
.
1.1.2 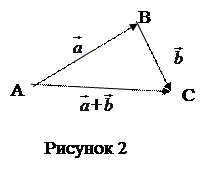 Определение. Суммой векторов
Определение. Суммой векторов 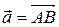 и
и 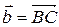 называется вектор, обозначаемый
называется вектор, обозначаемый  +
+ 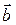 и равный
и равный 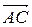 (рисунок 2).
(рисунок 2).
Итак,  +
+ 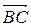 =
=  (правило треугольника).
(правило треугольника).
При решении задач полезно использовать свойства суммы векторов.
1.1.3  +
+ 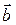 =
= 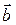 +
+  ,
, 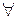
 ,
, 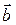 .
.
1.1.4  + (
+ (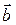 +
+ 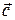 ) = (
) = ( +
+ 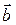 )+
)+ 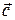 ,
, 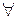
 ,
, 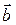 ,
, 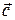 .
.
1.1.5 Существует единственный нулевой вектор 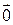 , имеющий нулевую длину и такой, что
, имеющий нулевую длину и такой, что 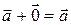 ,
, 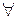
 .
.
1.1.6 Для любого вектора  существует единственный противоположный вектор (–
существует единственный противоположный вектор (–  ) такой, что
) такой, что 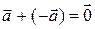 .
.
1.1.7 Определение. Произведением вектора  на действительное число
на действительное число 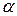 называется вектор
называется вектор 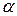
 (или
(или 
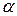 ), длина которого равна
), длина которого равна  , а направление совпадает с направлением
, а направление совпадает с направлением  , если
, если 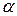 >0, и противоположно
>0, и противоположно  , если
, если 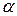 <0.
<0.
Перечислим свойства произведения вектора на число, которые постоянно используются при решении задач:
1)  ; ;
| 3) 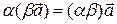 ; ;
| 5) 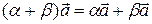 ; ;
|
2) 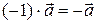 ; ;
| 4) 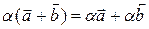 ; ;
| для любых  . .
|
1.1.8 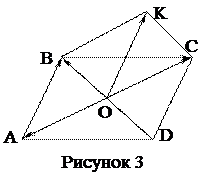 Пример. Пусть задан параллелограмм
Пример. Пусть задан параллелограмм 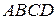 ,
, 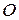 – точка пересечения его диагоналей (рисунок 3). Доказать, что
– точка пересечения его диагоналей (рисунок 3). Доказать, что
1) 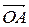 +
+ 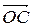 =
= 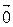 ; 3)
; 3) 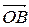 +
+ 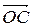 =
= 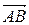 .
.
2) 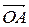 +
+ 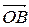 +
+ 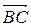 =
= 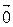 ;
;
Решение.
1 Известно, что диагонали параллелограмма вточке пересечения делятся пополам. Значит, 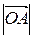 =
= 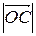 . Поскольку векторы
. Поскольку векторы 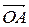 и
и  противоположно направлены, то
противоположно направлены, то 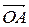 =−
=− 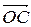 , т.е.
, т.е. 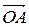 +
+  =
=  .
.
2 По определению суммы векторов 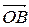 +
+ 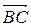 =
= 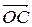 . С другой стороны
. С другой стороны 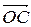 =−
=− 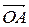 , поэтому
, поэтому 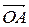 +
+ 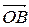 +
+ 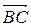 =
= 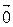 .
.
3 На векторах 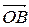 и
и  , как на сторонах, построим параллелограмм
, как на сторонах, построим параллелограмм  (см. рисунок 3). Тогда
(см. рисунок 3). Тогда  =
= 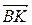 ,
, 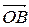 +
+  =
= 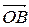 +
+ 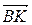 =
= 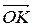 . Обратимся к четырехугольнику
. Обратимся к четырехугольнику 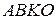 . Это параллелограмм, т.к.
. Это параллелограмм, т.к. 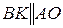 , и поэтому
, и поэтому 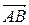 =
= 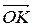 . Теперь очевидно, что
. Теперь очевидно, что 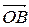 +
+  =
= 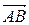 .
.
 2020-10-12
2020-10-12 134
134








