Считаем, что в пространстве задана ортонормированная система координат 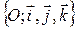 . Координаты произвольной точки M обозначаем, как правило, x,y,z, и пишем M (x,y,z). Вектор
. Координаты произвольной точки M обозначаем, как правило, x,y,z, и пишем M (x,y,z). Вектор  , параллельный прямой L, называют направляющим вектором этой прямой. Перечислим основные способы задания прямых в пространстве.
, параллельный прямой L, называют направляющим вектором этой прямой. Перечислим основные способы задания прямых в пространстве.
6.1.1 Прямая L определяется как линия пересечения плоскостей 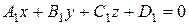 и
и 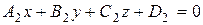 . Её уравнения имеют вид:
. Её уравнения имеют вид:
 (25)
(25)
Уравнения (25) называют общими уравнениями прямой L.
6.1.2 Прямая L определяется одной своей точкой  и направляющим вектором
и направляющим вектором 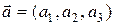 . Её уравнение имеет вид:
. Её уравнение имеет вид:
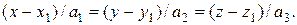 (26)
(26)
Уравнения (26) называют каноническими уравнениями прямой L.
6.1.3 Прямая L определяется одной своей точкой  и направляющим вектором
и направляющим вектором  . Она может быть задана параметрическими уравнениями вида:
. Она может быть задана параметрическими уравнениями вида:
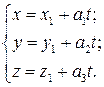 (27)
(27)
где t – параметр, 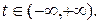
6.1.4 Прямая определяется двумя своими точками 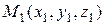 и
и 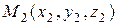 ,
, 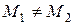 . Она может быть задана уравнениями следующего вида:
. Она может быть задана уравнениями следующего вида:
 (28)
(28)
6.1.5 Пример. Записать канонические и параметрические уравнения прямой, проходящей через точку 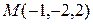 параллельно оси Ox.
параллельно оси Ox.
Решение. По условию искомая прямая L параллельна оси Ox, поэтому вектор  , расположенный на оси Ox, можно считать направляющим вектором прямой L. Согласно (26) получаем канонические уравнения прямой L:
, расположенный на оси Ox, можно считать направляющим вектором прямой L. Согласно (26) получаем канонические уравнения прямой L:
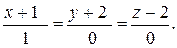
Заметим, что нули в знаменателях дробей в канонических уравнениях означают только то, что 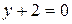 и
и 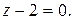 Согласно (27) получаем параметрические уравнения прямой L:
Согласно (27) получаем параметрические уравнения прямой L:
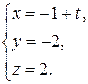
6.1.6 Пример. Прямая задана общими уравнениями:
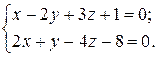
Записать канонические уравнения этой прямой.
Решение. Для того, чтобы записать канонические уравнения прямой L, требуется найти какую-либо точку на ней и её направляющий вектор или найти две различные точки этой прямой. Выберем точку на прямой L. Полагаем z= 0 в общих уравнениях прямой. Получаем систему уравнений:
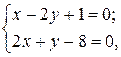 откуда x =3, y =2.
откуда x =3, y =2.
Итак, точка  принадлежит L. Направляющий вектор
принадлежит L. Направляющий вектор 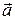 прямой L должен быть перпендикулярен обоим нормальным векторам
прямой L должен быть перпендикулярен обоим нормальным векторам 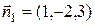 и
и 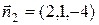 плоскостей
плоскостей 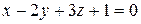 и
и 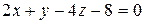 . Значит, в качестве направляющего вектора можно взять векторное произведение
. Значит, в качестве направляющего вектора можно взять векторное произведение 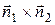 , т.е.
, т.е.
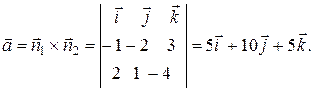
Согласно (26) записываем канонические уравнения L:
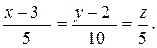
 2020-10-12
2020-10-12 147
147








